Aperçu des sections

  • Généralités

    Statistique3

    يعتبر مقياس الإحصاء3 امتدادا لم تم تناوله في الإحصاء 1 و2 وتمهيدا لدراسة الإحصاء 4، وهو بالأساس يهتم بدراسة مختلف النماذج الاقتصادية والإدارية وإعطاءها صيغ رياضية تسمح بحل المشكلات التي تصاف الباحث، وذلك من خلال التطرق إلى مختلف التوزيعات الاحتمالية الخاصة. لقد تضمن هذا الدرس أربعة فصول مرتبة من حيث المنهجية العلمية التي تساعد الطالب على تعلم أفضل أسس الإحصاء3، حيث تم التطرق في الفصل الأول إلى التوزيعات الاحتمالية المنفصلة من خلال فهم سلوك المتغير العشوائي وتوزيعه الاحتمالي استندادا لاحتماله المقابل، أما في الفصل الثاني فقد تم التطرق إلى فهم التوزيعات الاحتمالية المتصلة ومنها التوزيعات الخاصة الأكثر شهرة على غرار التوزيع الطبيعي، توزيع كاي مربع، توزيع ستيودنت وفيشر....في الفصل الثالث تناولنا فيه تقارب بعض التوزيعات الاحتمالية، وفي الأخير تضمن الفصل الرابع المتغيرات العشوائية الثنائية المنفصلة والمتصلة وأهم خواصها (المتغير العشوائي المنفصل الثنائي والدالة الهامشية، التوزيعات المشتركة المتصلة والدوال الهامشية...). وقد تضمن كل فصل مجموعة من التمارين والأمثلة التطبيقية التي تثبت الأهداف المرجوة من خلال هذا الدرس.

  • معلومات حول المقياس

    Statistique3

    • الأهداف العامة للمقياس

      يعتبر الإحصاء3 أحد فروع الإحصاء الرياضي الذي أصبحت له مكانة بارزة بين الدراسات الرياضية لما له من استخدامات تطبيقية واسعة ومفيدة في كل حقول البحث العلمي على العموم، خاصة في مجال اتخاذ القرار من الجانب الإداري والاقتصادي، كما أن أسلوب التنبؤ وتحديد الاتجاهات المستقبلية للعديد من الظواهر إنما يعتمد على مبادئ نظرية الاحتمالات. والإحصاء3 هو ذلك الإحصاء الذي يهتم بتحليل وفهم مختلف القوانين الاحتمالية الخاصة المنفصلة والمستمرة إضافة إلى المتغيرات العشوائية الثنائية في شقيها المنفصل والمتصل.

      الهدف الرئيسي لهذا المقياس هو:

      - التعرف على مختلف قوانين التوزيعات الاحتمالية المنفصلة والمتصلة (التوزيع الثنائي، توزيع بواسون، التوزيع الطبيعي، التوزيع الأسي....).

      - اكساب الطالب القدرة على تطبيق التوزيعات الاحتمالية لمعالجة وحل المشكلات الاقتصادية، الإدارية والاجتماعية.

      - استيعاب المتغيرات العشوائية الثنائية المنفصلة والمتصلة وأهم خواصها (المتغير العشوائي المنفصل الثنائي والدالة الهامشية، التوزيعات المشتركة المتصلة والدوال الهامشية...).

      - التعرف على التوزيعات ذات المتغيرين.

      بعد الانتهاء من دراسة هذا المقياس يتوقع من الطالب أن يحقق جملة من المهارات هي:

      - استيعاب الطالب للمفاهيم المتعلقة بالإحصاء الرياضي والقدرة على التمييز بين التوزيعات الاحتمالية الخاصة المنفصلة والمتصلة، والتمكن من حل المشكلات الاقتصادية والاجتماعية.

      - القدرة على حساب الاحتمالات وتوظيفها في مختلف التخصصات.

      - التمكن من إدراك الفرق بين قوانين التوزيعات الاحتمالية المنفصلة والمتصلة ومجالات استخدامها في الواقع العملي، وابتكار حلول جديدة لحل المشكلات الاقتصادية.

      - إكساب الطالب القدرة على التحليل الإحصائي باستخدام الأساليب الرياضية للوصول إلى النتائج المرجوة والقرارات الأكثر دقة، واكتساب القدرة على التواصل وتوضيح الفكرة بالمنطق السليم.


      • المكتسبات القبلية


        Statistique3

        للتمكن من متابعة مقياس إحصاء 3 يجب على الطالب أن يكون ملما بالعناصر التالية:

        الرياضيات: مفاهيم أساسية في الجبر، الدوال الأسية، التكامل، الاشتقاق...

        الإحصاء الوصفي: مقاييس النزعة المركزية (المتوسط، الوسيط، المنوال) ومقاييس التشتت (التباين، الانحراف المعياري، المدى).

        الاحتمالات: وتتضمن كل من (التجربة العشوائية، طرق تعيين الاحتمالات، مسلمات ودساتير الاحتمال، المتغيرات العشوائية المنفصلة والمستمرة...)


      • طريقة التقييم


        Statistique3

        يتم التقييم النهائي لهذا المقياس عبر طريقتين هما:

        امتحان نهائي: ويكون هذا الامتحان شامل لجميع ما تم دراسته من خلال الفصول خلال السداسي، ويجسد هذا الامتحان نسبة 60% من العلامة النهائية.

        المراقبة المستمرة: يجسد هذا التقييم نسبة 40% المتبقية، ويسمح هذا التقييم باكتساب مجموعة من النقاط خلال السداسي وتكون المراقبة المستمرة بعدة طرق وأشكال تسمى بوزن الأعمال الموجهة، وحسب اللجنة الوزارية المتخصصة في شعبة العلوم الاقتصادية، التجارية وعلوم التسيير فقد تم وضع المعايير التالية:

        علامة خاصة بالامتحان الجزئي في حدود 6 نقاط تمثل 12% من الوزن النسبي للأعمال الموجهة.

        علامة خاصة بالحضور والمواظبة في حدود 6 نقاط تمثل 12% من الوزن النسبي للأعمال الموجهة.

        علامة خاصة بإنجاز الواجبات والمشاريع البحثية في حدود 4 نقاط تمثل 8% من الوزن النسبي للأعمال الموجهة.

        علامة خاصة بالمشاركة وحسن السلوك في حدود 4 نقاط تمثل 8% من الوزن النسبي للأعمال الموجهة.

        يدرس المقياس في شكل محاضرات وأعمال موجهة وطبيعة تقييمها امتحان ومراقبة مستمرة، يقاس معدل المقياس بالوزن الترجيحي للمحاضرة والأعمال الموجهة.

        • المخطط العام للمقياس

          يتناول هذا المقياس الإحصاء3 (الإحصاء الرياضي) وذلك لتمكين الطالب من مواصلة مساره الدراسي في كل تخصصات العلوم الاقتصادية، ويعتبر أحد أهم المعارف التي يجب أن تكتسب لدراسة عدة مقاييس أخرى في السداسيات القادمة كالإحصاء4، الاقتصاد القياسي وتحليل البيانات الإحصائية. من الناحية البيداغوجية فقد حاولنا من خلال فهم محتوى هذا المقياس الاعتماد على أربعة فصول شاملة تتمثل فيمايلي:

          - الفصل الأول: قوانين التوزيعات الاحتمالية المنفصلة (توزيع برنولي، توزيع ذي الحدين، توزيع بواسون، التوزيع الهندسي، التوزيع فوق الهندسي)

          - الفصل الثاني: قوانين التوزيعات الاحتمالية المتصلة (التوزيع الطبيعي، التوزيع المنتظم، التوزيع الأسي، توزيع كاما، توزيع بيتا، توزيع كاي تربيع، توزيع ستيودنت، توزيع فيشر)

          - الفصل الثالث: تقارب بعض التوزيعات الاحتمالية

          - الفصل الرابع: المتغيرات العشوائية الثنائية المنفصلة والمتصلة وأهم خواصها (المتغير العشوائي المنفصل الثنائي والدالة الهامشية، التوزيعات المشتركة المتصلة والدوال الهامشية...).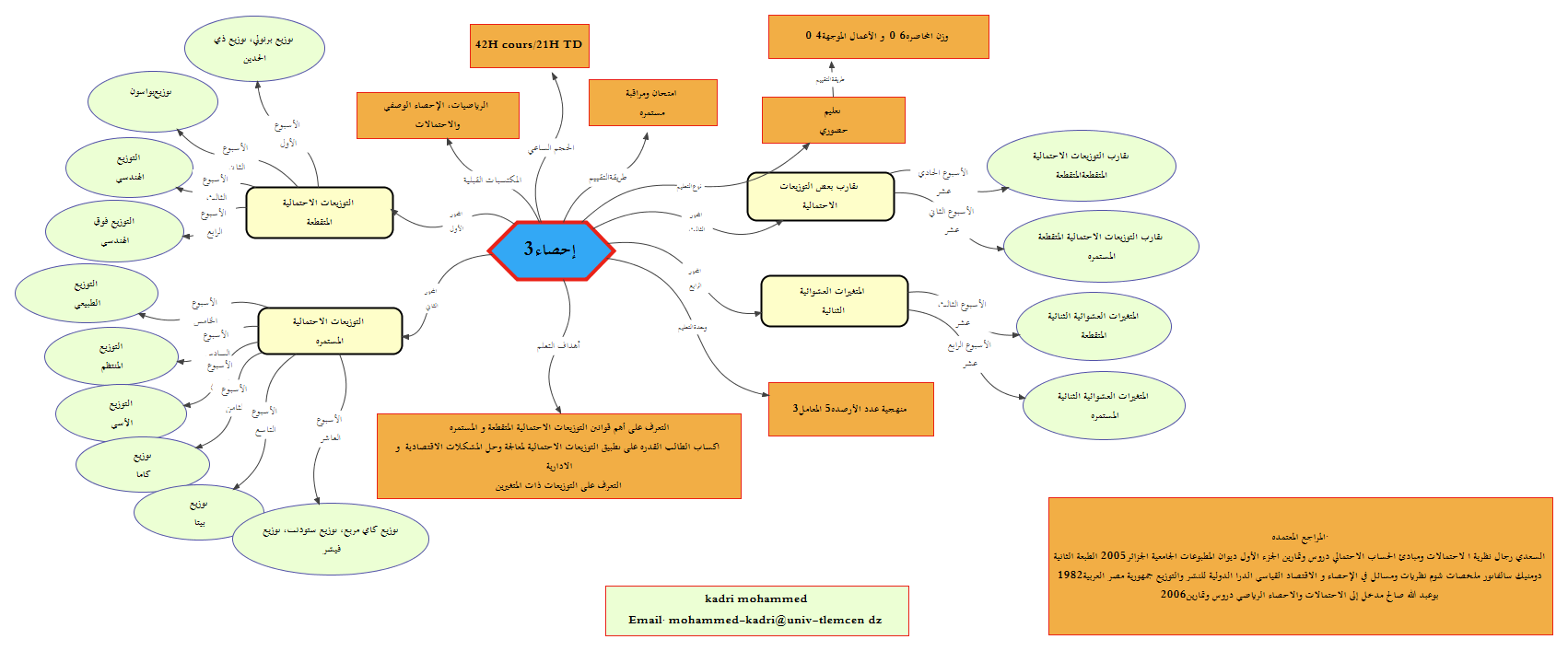

          Statistique3


        • الفصل الأول

        • TD 1

        • الفصل الثاني

        • TD 2

        • الامتحان النهائي

        • المراجع البيبليوغرافية

          من أجل التمكن الجيد من المقياس واكتساب المهارات والمتطلبات المرجوة لابد للطلبة الاطلاع على مختلف المصادر المساعدة على ذلك ونضع تحت تصرفهم مجموعة من الكتب وذلك لضمان السيرورة الجيدة لاكتساب كل الكفاءات المستهدفة:

          1.    السعدي رجال(2005) نظرية الاحتمالات ومبادئ الحساب الاحتمالي: دروس وتمارين -الجزء الأول-ديوان المطبوعات الجامعية، الطبعة 02، الجزائر.

          2.    دومينيك سالفاتور، ترجمة سعدية حافظ منتصر (1982) ملخصات شوم، نظريات ومسائل في الإحصاء والاقتصاد القياسي، الدار الدولية للنشر والتوزيع، جمهورية مصر العربية.

          3.       على عبد السلام العماري وعلي حسين العجيلي(2000) الإحصاء والاحتمالات: النظرية والتطبيق، منشورات (ELGA)، مالطا.

          4.    بوعبد الله صالح (2000) مدخل إلى الاحتمالات والإحصاء الرياضي: دروس وتمارين.

          5.    عبد الحميد ربيع غيطان (2004) نظرية الاحتمالات: الجزء الثاني، دار الكتب الأكاديمية، الطبعة الأولى، مصر.

          6.    محمد كبيه وماهر بدوي (2003) الإحصاء التطبيقي، منشورات جامعة حلب، كلية الاقتصاد.


          • Section 12

            • Section 13

              • Section 14