Diffraction des ondes lumineuses
But
Le but du TP est le suivant :
- Mettre en évidence le phénomène de diffraction des ondes lumineuses, étudier l'influence de différents paramètres sur la figure de diffraction, et déterminer les conditions nécessaires à la diffraction,
- Mettre en évidence le phénomène d'interférences des ondes lumineuses.
Définition
La diffraction par une longue fente étroite
On appelle diffraction le phénomène selon lequel une onde, lorsqu'elle traverse une petite ouverture ou rencontre un petit objet, change de direction sans modification de sa fréquence ou de sa longueur d'onde. Ce phénomène est d'autant plus marqué que la taille de l'obstacle ou de l'ouverture est réduite.
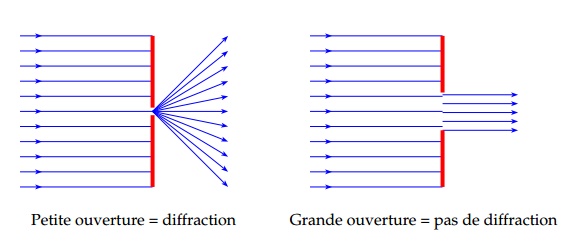
Pour que le phénomène de diffraction se manifeste, il est nécessaire que la taille de l'obstacle ou de l'ouverture soit du même ordre de grandeur que la longueur d'onde de l'onde incidente.
Soit une diffraction causée par un faisceau laser étroit passant à travers une fente verticale de dimensions comparables à sa propre longueur d'onde. Le faisceau se diffracte en formant des tâches lumineuses séparées par des régions sombres appelées extinctions. La tâche centrale présente une taille plus importante et une intensité lumineuse plus élevée que les autres. En s'éloignant du centre vers la périphérie, la taille et l'intensité des tâches diminuent.
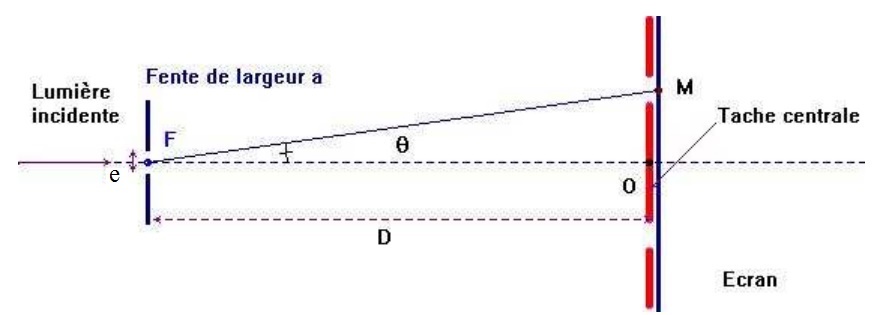
Dans les conditions de Fraunhofer (qui correspondent à la diffraction d'une onde plane à une grande distance de l'ouverture ou près de l'image géométrique de la source lumineuse), la distribution des intensités est donnée par :
\( I(\theta)=I_0 \frac {sin^2 ~ \left( \frac{\pi e}{\lambda} sin ~ \theta \right) }{\left( \frac{\pi e}{\lambda} sin ~ \theta \right)^2 } \) (1)
Conditions des minimums :
\( I(\theta)=0 \) lorsque\( \frac{\pi e}{\lambda} sin ~ \theta = \pm n \pi \) Le premier minimum est tel que \( n=1 \)
Mais \( \theta \) petit \( \Rightarrow sin~\theta \approx \theta \approx tg \theta=\frac{x}{D} \) donc:
\( h=\frac{2 \lambda D}{e} \) (2)
Où \( h = 2x \) est la largeur de la tâche centrale.
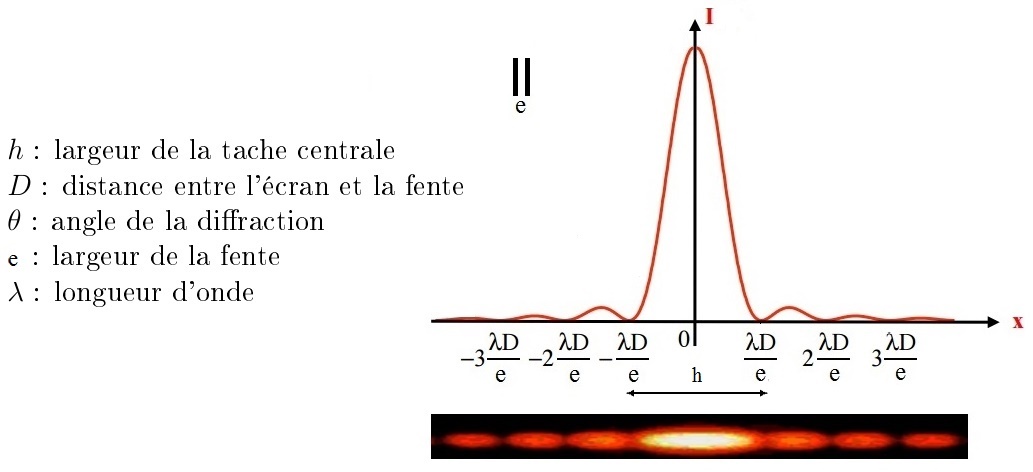
La diffraction par deux fentes parallèles identiques
Interférences lumineuses
Les phénomènes d'interférences résultent de la superposition de deux ondes lumineuses. Ils ne peuvent se produire que lorsque les conditions suivantes sont réalisées :
- Les ondes sont cohérentes.
- Elles ont la même fréquence, donc la même longueur d'onde.
- Elles sont parallèles.
- Elles ont la même amplitude, ou presque.
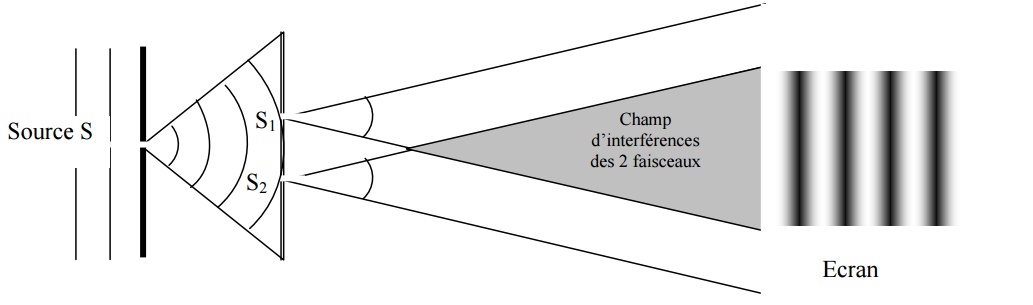
Soit S une source ponctuelle monochromatique éclairant deux fentes \( S_1 \) et \( S_2 \) proches l'une de l'autre, mais assez éloignées de \( S\). \( S_1 \) et \( S_2 \) jouent le rôle de sources cohérentes, c'est-à-dire qu'elles sont dans le même état vibratoire. \( S_1 \) et \( S_2 \) diffractent la lumière. Dans la région de l'espace où les deux faisceaux se superposent, on peut observer une succession de franges brillantes et de franges sombres.
La distribution de l'intensité sur le plan d'observation est donnée par :
\( I=I_0 \cdot \frac {sin^2 ~ \left( \frac{\pi e}{\lambda} sin ~ \theta \right) } { \underbrace{\left( \frac{\pi e}{\lambda} sin ~ \theta \right)^2}_{Terme~ de ~diffraction} } \cdot \underbrace{ cos^2 \left( \frac{\pi a sin ~ \theta}{\lambda}\right) } _{Terme~ d'interférence} \) (3)
Les maximums d'intensité "principaux" distants de \( h \) correspondant à la diffraction satisfont à la même condition que les minimums pour une fente ou deux fentes. \( h=\frac{2 \lambda D}{e} \)
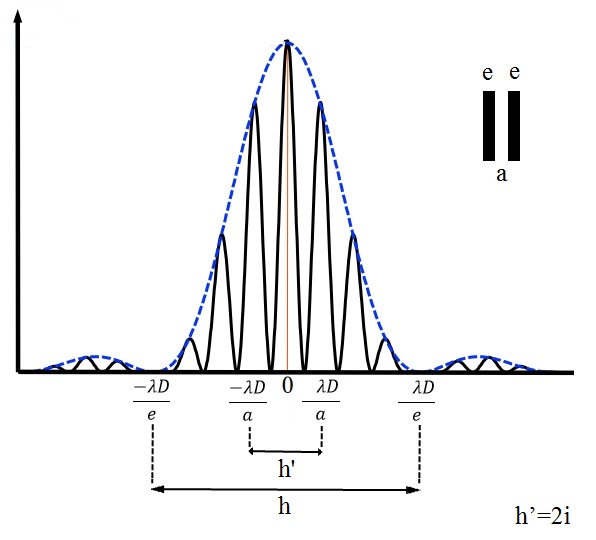
Les positions des maximums correspondant à l'interfrange sont alors données par :
\( \frac{\pi a} {\lambda} sin~ \theta =\pm m \pi~~~~~m=0,1,2... \) ordre du maximum principale. \( \theta \) très petit.
\( \Rightarrow sin~ \theta \approx \theta \approx tg~ \theta \approx \frac{h'}{2D}$ d'où $\frac{\pi a}{\lambda} sin~ \theta = \frac{\pi a}{\lambda} \left( \frac{h'}{2D}\right) = \frac{\pi a i}{\lambda D}=\pm m \pi . \)
La distance \( i \) entre deux franges brillantes consécutives est :
\( i=\frac{\lambda D}{a} \) (4)
Diffraction par N fentes identiques : le réseau
C'est un système de \( N \) fentes parallèles équidistantes et identiques. On observe la même distribution qu'avec deux fentes mais avec un nombre de franges d'interférences différent.
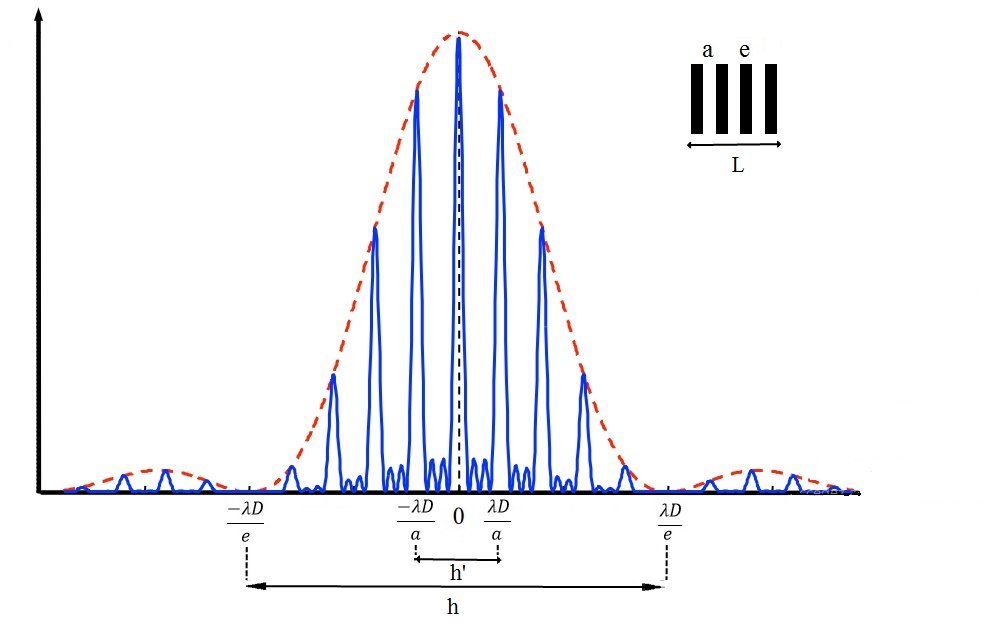
\( I=I_0 \cdot \frac {sin^2 ~ \left( \frac{\pi e}{\lambda} sin ~ \theta \right) } { \underbrace{\left( \frac{\pi e}{\lambda} sin ~ \theta \right)^2}_{Terme~ de ~diffraction~ (Enveloppe)} } \cdot \underbrace{ \frac{sin^2 ~ \left( \frac{N \pi a}{\lambda} sin ~ \theta \right) }{sin^2 ~ \left( \frac{\pi a}{\lambda} sin ~ \theta \right) } } _{Interférences~ entre ~les~ différentes ~ondes} \) (5)
Les minimums d'intensité "principaux" distants de \( h \) correspondant à la diffraction satisfont à la même condition que les minimums pour une fente ou deux fentes.
\( h=\frac{2 \lambda D}{e} \) (6)
L'interfrange est alors donnée comme pour deux fentes par :
\( i=\frac{\lambda D}{a} \) (7)
Manipulation
L'étude expérimentale sera réalisée avec un laser émettant une lumière monochromatique de longueur d'onde \( \lambda = 0,633 \) µm.
On observe l'image de diffraction sur un écran distant de \( D = 3,20 \) m.
La diffraction par une longue fente étroite
Pour mettre en évidence le phénomène de diffraction de la lumière, vous pouvez réaliser un montage simple en utilisant un laser et une fente fine. Voici les étapes pour réaliser ce montage :
- Placez le laser sur une surface stable de manière à ce qu'il soit dirigé vers la fente.
- Fixez la fente à une certaine distance du laser, en vous assurant qu'elle est bien alignée avec le faisceau lumineux du laser.
- Placez l'écran de projection à une distance \( D \) de la fente, comme indiqué précédemment.
- Allumez le laser et observez l'image de diffraction formée sur l'écran.
Effectuer la mesure de \( h \), Déduire la largeur e de la fente.
Calculer les erreurs.
La diffraction par deux fentes parallèles identiques
Cette partie nous intéresser à la diffraction d’un même faisceau monochromatique
par deux fentes. Il se produit, en plus de la simple diffraction du faisceau,
un phénomène interférences.
Effectuer la mesure de \( h \) et de \( i \)
Déduire \( e \) et \( a \).
Calculer les erreurs.
Diffraction par N fentes identiques : le réseau
L'objectif de cette manipulation est de généraliser le dispositif des fentes d'Young (dispositif à deux fentes) afin de comprendre le fonctionnement des dispositifs à fentes multiples régulièrement espacées et de même largeur.
Effectuer la mesure de \( h \) et de \( i \)
Déduire \( e \) et \( a \).
Connaissant la largeur L du réseau à \( N\) fentes, déterminer \( N= \frac{L}{a} \)
Calculer les erreurs.
On donne \( L=36 mm \)
