Reflexion-Refraction
Définition
Vitesse de propagation de la lumière
Dans le vide, la lumière se propage en ligne droite à la vitesse c qui est, par définition, la suivante:
\( c = 299792458~m.s^{-1} \simeq 3,108~m.s^{-1} \)
Indice optique
Par contre l'expérience montre que la vitesse de propagation de la lumière change d'un milieu matériel à l'autre, et qu'elle est toujours inférieure à \( c \). On définit alors l'indice de réfraction n d'un milieu comme étant égal au rapport de la vitesse de la lumière dans le vide, à la vitesse v de la lumière dans le milieu considéré:
\( n = \frac{c}{\nu} \)
L'indice du vide est donc égal à l'unité, tandis que l'indice des substances transparentes dans le visible est supérieur à l'unité. Retenons les valeurs des indices des milieux suivants:
- indice de l'air: \( 1,0003 \)
- indice du verre: \( 3/2 \)
- indice de l'eau: \( 4/3 \).
Un dioptre
Est une surface qui sépare deux milieux transparents et homogènes d'indices optiques différents, par exemple l'interface eau/air définie par la surface libre de l'eau d'un lac.
Miroir
Est une surface réfléchissante telle que pratiquement toute la lumière incidente est renvoyée par la surface.
Lois de Snell-Descartes
Réflexion
Lorsqu'un rayon arrive à l'interface entre deux milieux isotropes et homogènes différents, il donne naissance à un rayon réfléchi et à un rayon transmis (réfracté).
On définit le plan d'incidence comme le plan contenant le rayon incident et la normale à l'interface (Figure 1). L'angle d'incidence \( i_1 \) est l'angle que forme le rayon incident avec la normale.
Lois de la réflexion
- Le rayon réfléchi est dans le plan d'incidence. On définit alors l'angle de réflexion \( i'_1 \)
- Le rayon réfléchi est symétrique du rayon incident par rapport à la normale:
\( i_1 = i'_1~~~~~~(1) \)
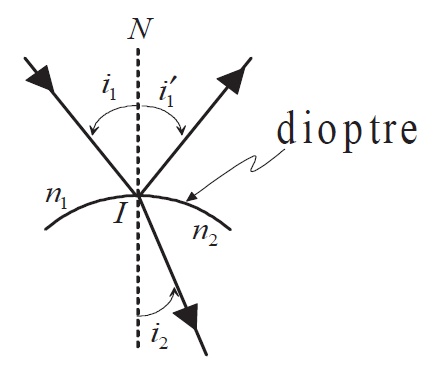
Figure 1: Lois de Snell-Descartes
Réfraction
La réfraction est la déviation de la lumière lorsqu'elle traverse l'interface entre deux milieux transparents d'indices optiques différents (Figure 1).
Lois de la réfraction
- Le rayon réfracté est dans le plan d'incidence. On définit alors l'angle de réfraction\( i_2 \).
- Le rayon réfracté est tel que:
\( n_1~sin~ i_1 = n_2~ sin ~i_2 \)
Cas où \( n_1< n_2 \): réfraction limite
Le rayon lumineux passe du milieu 1 moins réfringent au milieu 2 plus réfringent (Figure 2). Nous avons alors
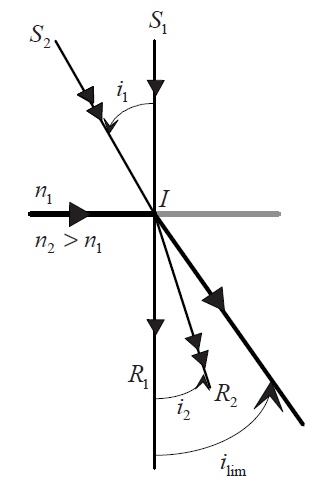
Figure 2 : Réfraction limite
\( n_1~sin~ i_1 = n_2~ sin ~i_2 \) avec \( n_2>n_1 \):
Il en résulte que sin i2 < sin i1 ; les angles i1 et i2 étant compris entre 0 et π /2 , sinus et angles varient dans le même sens, soit i2 < i1. Le rayon réfracté se rapproche donc de la normale.
Un rayon incident normal (\( S_1 I \)), pour lequel \( i_1 = 0 \), entre sans déviation (\( IR_1 \) tel que i_2 = 0 ). Lorsque \( i_1 \) croît, \( i_2 \)croît aussi tout en restant inférieur à \( i_1 \). A l'incidence rasante (\( i_1 =\pi /2 \)), l'angle de réfraction est maximal (angle de réfraction limite noté \( i_{lim} \)) et vaut:
\( sin ~ i_{lim} =\frac{n_1}{n_2}~~~~~~(3) \)
Cas où \( n_1>n_2 \): réflexion totale
Le rayon lumineux passe maintenant du milieu 1 plus réfringent au milieu 2 moins réfringent. La troisième loi de Snell-Descartes implique alors que
\( i_1 < i_2 \)
Le rayon réfracté s'écarte donc de la normale et l'angle de réfraction est maximal
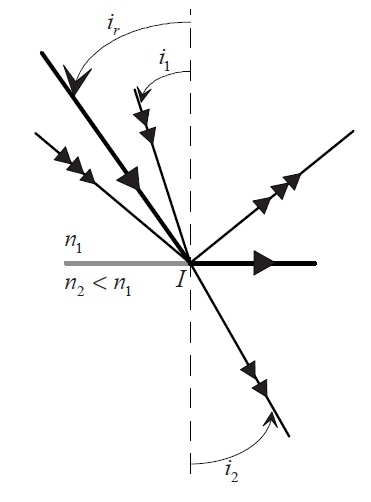
Figure 3: Réflexion totale
(\( i_2 = \pi/2 \)) pour un angle d'incidence limite\( i_r \) tel que:
\( sin~i_r =\frac{n_2}{n_1}~~~~~~(4) \)
Si l'angle d'incidence est supérieur à ir, il n'y a plus de rayon réfracté (en effet, on a alors sin i2 > 1, \( i_2 \)n'est donc plus défini), le rayon incident est totalement réfléchi : on parle de réflexion totale. Le dioptre se comporte comme un miroir (Figure 3).
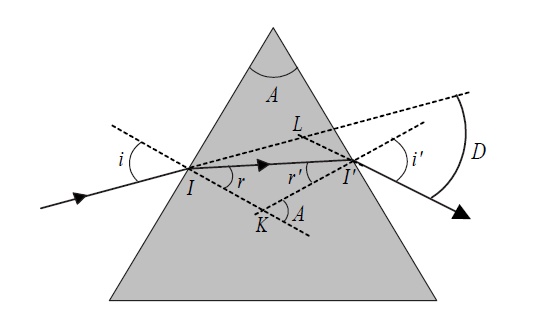
Le prisme
La déviation minimale est le plus petit angle \( D \) formé par la réfraction de la lumière incidente et la lumière émergente. La formule reliant \( D \) à i n'est pas aisée à démontrer, on peut cependant remarquer que la déviation \( D \) passe par un minimum, Dmin, obtenu, avec les notations de la figure 4, pour \( i_1 = r_2 \) et \( i_2 = r_1 \) (symétrie entre l'entrée et la sortie), ce qui conduit en utilisant les relations angulaires dans le prisme et la loi de Snell-Descartes, à:
\( n=\frac{sin~ [(A+D)/2}{sin~ (A/2)}~~~~~~~(5) \)
Figure 4: Trajet des rayons lumineux traversant un prisme
Manipulation
Réflexion
Placer le miroir plan au centre du disque gradué. Faire varier l'angle d'incidence ( de 10° en 10°) et noter l'angle de réflexion. Que peut-on en conclure.
\( \begin{array}{|l|l|l|l|l|l|l|l|l|}
\hline
~~i_1 (^\circ)~~&~~10~~&~~20~~&~~30~~& ~~40~~&~~50~~&~~60~~&~~70~~&~~80~~\\
\hline
~~i_2 (^\circ)~~&&&&&&&&\\
\hline
\end{array} \)
Réfraction
Première partie
Placer le demi-cylindre de plexiglas d'indice n au centre du disque gradué (côté plan face à la lumière). Faire varier l'angle d'incidence. Noter l'angle de réfraction. Déduire n.
\( \begin{array}{|l|l|l|l|l|l|l|l|l|}
\hline
~~i_1(^\circ)~~&~~10~~&~~20~~&~~30~~& ~~40~~&~~50~~&~~60~~&~~70~~&~~80~~\\
\hline
~~i_2 (^\circ)~~&&&&&&&&\\
\hline
\end{array} \)
Observez le rayon réfracté, puis mesurer l'angle limite de réfraction limite (lorsque \( i_2= \pi/2 \)) en déduire l'indice de plexiglas.
Déterminer l'indice du plexiglas avec son incertitude par les valeurs moyennes des mesures.
Déterminer l'indice du plexiglas avec son incertitude par la courbe \( sin~i_1=F~(sin ~i_2) \).
Comparer ces résultats et que peut-on en conclure.
Deuxième partie
Placer le demi-cylindre de plexiglas d'indice n au centre du disque gradué (côté sphérique face à la lumière). Faire varier l'angle d'incidence. Noter l'angle de réfraction. Déduire \( n \).
\( \begin{array}{|l|l|l|l|l|l|l|l|l|}
\hline
~~i_1 (^\circ)~~&~~10~~&~~20~~&~~30~~& ~~40~~&~~50~~&~~60~~&~~70~~&~~80~~\\
\hline
~~i_2 (^\circ)~~&&&&&&&&\\\hline
~~n~~&&&&&&&&\\
\hline
\end{array} \)
Observez le rayon réfracté, puis mesurer l'angle limite de réfraction limite (lorsque \( i_2= \pi/2 \)) en déduire l'indice de plexiglas.
Déterminer l'indice du plexiglas avec son incertitude par les valeurs moyennes des mesures.
Déterminer l'indice du plexiglas avec son incertitude par la courbe \( sin~i_1=F~(sin ~i_2) \).
Comparer ces résultats et que peut-on en conclure.
Mesure de l'indice d'un liquide
Mesurer maintenant l'indice du liquide renfermé dans une cuve prismatique.
Placer la cuve prismatique (milieu d'une face) au centre du disque gradué et mesurer la variation minimale. Refaire la même chose pour les deux autres faces et prendre la valeur moyenne de \( D \).
Déterminer l'indice du liquide renfermé dans la cuve avec son incertitude.