Cycle d'hystérésis d'un matériau ferromagnétique forme de tige
L'objectif de ce TP est de déterminer le cycle d'hystérésis et la perméabilité d'un matériau ferromagnétique forme de tige.
Étude Théorique
Les propriétés magnétiques des matériaux jouent un rôle important dans les machines et les appareils électriques comme les moteurs, les transformateurs. Leur rôle est prépondérant dans le stockage de l'information (bande d'enregistrement HiFi, disque dur d'ordinateur) qui se fait par l'intermédiaire d'un substrat doté de propriétés magnétiques spécifiques.
Le magnétisme dans la matière
Sous l'effet d'un champ magnétique extérieur \( \vec{H} \), il se crée dans les matériaux un champ d'induction magnétique \( \vec{B} \) dont la valeur est donnée par:
\( \vec{B}= \mu_0 \vec{H}~~~~~~~~(1) \)
où \( \mu_0=4 \pi \cdot 10^{-7} H m^{-1} \) est la perméabilité absolue du vide s'exprimant en \( henry\) par \( m\) (\( H m^{-1}\)). L'unité d'induction magnétique est le tesla (\( T\)) et le champ magnétique \( \vec{H} \), qui est en général créé par la circulation d'un courant électrique dans un solénoïde, s'exprime en ampère par mètre (\( A m^{-1}\)).
L'induction magnétique dans la matière peut également être exprimée par:
\( \vec{B}= \mu_0 (\vec{H}+\vec{M}) ~~~~~~~~(2) \)
L'allure générale de la courbe de dépendance de \( B\)en fonction de \( H\) dans la matière est représentée dans la figure 1. Cette courbe montre que l'induction \( B\) tend vers une valeur limite \( B_s\) dite valeur de saturation. On distingue deux zones: une zone linéaire \( (a)\) et une zone de saturation \( (b)\).
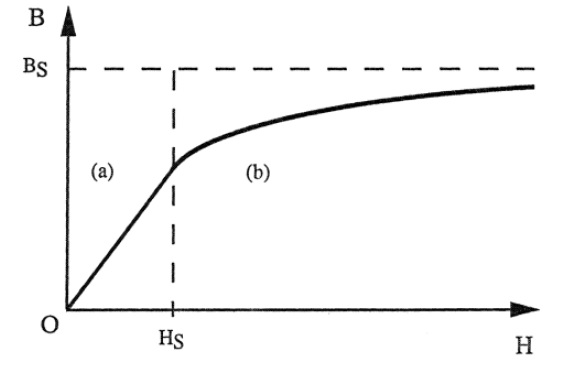
Figure 1 – L’induction magnétique en fonction du champ magnétique dans la matière
La zone linéaire \( H < H_s \), on peut écrire :
\[ \vec{M} =\chi_r \vec{H} ~~~~~~~~(3) \]
\[ \vec{B} = \mu_0 \vec{H} (1 + \chi_r ) ~~~~~~~~(4) \]
En comparant l'équation 3 et 4 on obtient, pour la perméabilité magnétique, l'expression suivante:
\[ \mu= \mu_0 (1 + \chi_r ) ~~~~~~~~(5) \]
où \(\chi_r\) représente la susceptibilité magnétique relative. Cette grandeur, qui est sans dimension, est reliée à la perméabilité relative \(\mu_r\) par:
\[ \mu_r= 1 + \chi_r ~~~~~~~~(6) \]
La zone de saturation \( H>H_s \):
Dans cette zone \(\vec{M}\) n'est plus une fonction linéaire de \(\vec{H}\). On peut cependant définir localement une valeur plus générale \(\mu^*_r\) de la perméabilité magnétique, en considérant des accroissements de \(\vec{B}\) et \(\vec{H}\) :
\[ d \mid \vec{B}\mid=\mu_0 \mu_r^* d\mid \vec{H}\mid ~~~~~~~~(7) \]
donc:
\[ \mu_r^*=\frac{1}{\mu_0} \frac{d \mid \vec{B}\mid} {d \mid \vec{H}\mid} ~~~~~~~~(8) \]
Classification magnétique des matériaux
On peut assimiler la circulation de l'électron sur son orbite à un courant électrique circulant dans une spire. La circulation de l'électron engendre un moment magnétique perpendiculaire au plan de l'orbite. L'intensité de ce moment magnétique est mesurée par le nombre quantique magnétique \(m_l\). De même, la rotation (spin) de l'électron sur lui-même engendre également un moment magnétique qui est quantifié par le nombre magnétique de spin \(m_s\) qui peut prendre deux valeurs distinctes (\(+\frac{1}{2}\) et \(-\frac{1}{2}\) ) quand \(m_s=+\frac{1}{2}\) , le moment magnétique est parallèle au champ magnétique. Si \(m_s=-\frac{1}{2}\) , le moment magnétique est orienté dans une direction opposée à celle du champ magnétique.
À l'état solide, ce sont seulement les atomes qui auront une couche électronique interne incomplète qui ont un moment magnétique permanent, car la couche électronique externe (électron de valence) est complétée par les électrons de valence des atomes voisins.
Suivant leur nature, on peut diviser les matériaux en cinq comportements magnétiques très différents:
- diamagnétique,
- paramagnétique,
- ferromagnétique,
- antiferromagnétique,
- ferrimagnétique.
Les matériaux diamagnétiques
On appelle diamagnétiques les substances qui présentent une aimantation \(M\) proportionnelle au champ \(H\) dans lequel elles sont placées et de sens opposé à celui-ci. La susceptibilité de ces corps est négative et faible, de l'ordre de \(10^{-6}\) , c'est-à-dire que la substance s'aimante en sens inverse du champ magnétisant.
Les matériaux paramagnétiques
On appelle paramagnétiques les substances qui présentent une aimantation \(M\) proportionnelle au champ \(H\) dans lequel elles sont placées et de même sens que lui. Pour ces substances, \(\chi _r\) est positive et faible et de l'ordre de (\(10^{-6}\) ).
Les matériaux ferromagnétiques
Tous les dipôles sont alignés de manière parallèle dans les différents domaines,la perméabilité magnétique reste très élevée (\(10^{3}<\chi _r< 10^{6}\)).
Les matériaux antiferromagnétiques
Les moments magnétiques atomiques sont égaux et se disposent suivant un mode antiparallèle. Ces matériaux ne possèdent jamais de moment magnétique permanent et leur susceptibilité est faible.
Les matériaux ferrimagnétiques
Les moments magnétiques des atomes sont inégaux et forment des domaines où ils sont alignés de manière antiparallèle.
Cycle d'hystéresis
Le cycle d'hystérésis est la courbe de réponse des matériaux magnétiques, à travers laquelle, ils gardent la mémoire de tous leurs états d'aimantation antérieurs par l'intermédiaire des domaines élémentaires.
Supposons un barreau ferromagnétique qui n'a jamais été aimanté et traçons la courbe d'induction \(B\) en fonction du champ \(H\).
Partant d'un champ nul \(0\), l'induction apparait avec un certain retard. Elle augmente ensuite rapidement, puis de moins en moins vite. Si l'on augmente encore l'intensité du champ, on constate que l'induction conserve une valeur stable à partir d'un certain état: c'est le phénomène de saturation. Nous obtenons ainsi la branche \(O A\) qui est la courbe de première aimantation.
Diminuons progressivement le champ magnétique \(H\) jusqu'à \(0\) où il devient nul. L'induction diminue en même temps, mais elle ne reprend pas au cours de cette période décroissante du courant les mêmes valeurs qu'elle avait pendant sa période croissante: on constate qu'elle n'est plus nulle. L'induction possède encore la valeur \(B_r\) qui représente l'aimant ation rémanente. C'est cette aimantation rémanente qui fait qu'un barreau ferromagnétique qui a été placé dans un champ magnétique conserve une certaine aimantation.
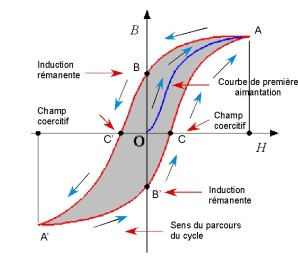
Figure 2 – Cycle d’hystéresis
En inversant le sens du courant, c'est-à-dire le sens du champ magnétisant, nous tracerons ainsi la branche \(BC'A'\). Au point \(C'\) l'induction est nulle. La valeur \(OC\) représente la force coercitive appelée également Champ coercitif. Le champ coercitif représente donc la valeur du champ magnétique nécessaire pour ramener à 0 l'induction rémanente en un point d'un corps magnétique lorsque celui-ci a été soumis à un nombre suffisant de cycles d'aimantation.
Un aimant est intéressant lorsque sa force coercitive et son intensité d'aimantation sont élevées. Toutefois un fort magnétisme rémanent reste sans intérêt lorsque le champ coercitif est faible. L'aimant que l'on pourrait constituer serait puissant mais le moindre champ inverse le démagnétiserait.
En faisant décroître de nouveau le champ jusqu'à 0, l'aimantation diminue jusqu'à une valeur représentée par 0 \(B'\) qui est l'aimantation rémanente. Le courant changeant alors de sens (\(B'C\)), l'aimantation rémanente est détruite. Puis le courant augmentant, l'aimantation croît jusqu'à A suivant la courbe \( CA\), nous ramenant ainsi au point de départ.
Travail expérimental
Remarque concernant la manipulation
- Lorsqu'on place un barreau ferromagnétique, jamais soumis auparavant à un champ magnétique, à l'intérieur d'un solénoïde, dont la longueur \(L\) est grande par rapport à son diamètre, pour un nombre de spires \(N\) , ce barreau de fer s'aimante: le champ magnétique de ce solénoïde est alors bien supérieur à celui qu'on obtiendrait dans un solénoïde vide.
\[ H=\frac{N}{L} I ~~~~~~~~(9) \]
- Si le barreau ferromagnétique possède déjà un aimentation rémanente, il faut le désaimanter, en faisant circuler à travers les spires du solénoïde un courant alternatif.
- Quand vous êtes sur un courant I (par exemple \(300~mA\)), NE RETOURNEZ JAMAIS AU COURANT PRÉCÉDENT.
Montage expérimental et mode opératoire
On peut voir sur la figure le schéma électrique du montage expérimental. Le but est de pouvoir alimenter la bobine avec un courant continu depuis \(0~A\) jusqu'à \(2~A\), avec possibilité d'en changer le sens.
- On mesure directement le courant \(I\) la valeur du champ magnétique \(B\) avec le Tesla-mètre
- Tracez le cycle d'hystérisis B=f(I).
- Observez les domaine de saturation, l'existence d'une aimentation rémanent et d'un champ coercitif.
