Diélectrique dans un condensateur à plaque
L'objectif de ce TP est de mesurer statique la tension V sur un condensateur à plaque pour différents diélectriques avec écart de plaque fixe \(d\) et la définition des constantes de diélectricité \(\varepsilon _r\) de différents matériaux.
Dispositif expérimental
- Condensateur à plaque \(d=260~mm\) et \(S=0.0531~ m^2\),
- Alimentation \(300 ~V\) ,
- Amplificateur électromètre,
- Condensateur \(228 ~nF\),
- voltmètre,
- Commutateur inverseur,
- Câbles d'expérience.

Étude Théorique
Définition
les isolants ou diélectriques sont des matériaux ayant une résistivité très élevée, car il contiennent très peu d'électrons libres. Un bon isolant ne devrait pas laisser passer de courant lorsqu'il est soumis à une tension continue.
Caractéristiques diélectrique des isolants
Un diélectrique est un matériau non conducteur ou faiblement conducteur, sans porteur de charge à déplacement libre, qui est traversé par un champ électrique. Il peut s'agir d'un gaz, d'un liquide ou d'un solide. Le condensateur à plaques est le type de condensateur le plus simple, il est constitué de deux conducteurs placés à proximité l'un à l'autre, mais sans qu'il y ait contact entre eux. Les conducteur permettent d'emmagasiner des charger électrique.
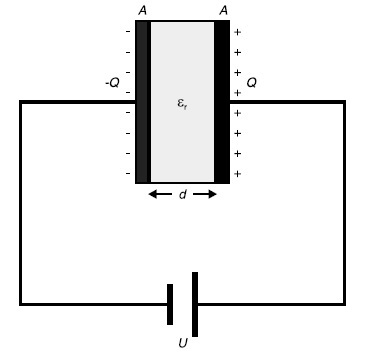
Si une différence de potentiel \(U\) est établie entre deux conducteurs semblables, ils acquièrent une charge égale et opposée de \(+Q\) et \(-Q\), respectivement. Pour un condensateur donnée, la quantité de charge \(Q\) sur chaque conducteur est proportionnelle à la différence de potentiel entre les conducteurs.
\[ Q=C.U~~~~~~~~(1) \]
La constante de proportionnalité \(C\) est appelée la capacité du condensateur. L'unité SI de la capacité est le Farad (F) qui vaut un Coulomb par volte (C/V).
La constante de diélectricité
La constante de diélectricité ou permittivité relative \(\varepsilon_r\) du diélectrique est indiquée par la relation entre le champ électrique \(E\) et le déplacement diélectrique \(D\):
\[ D= \varepsilon_r. \varepsilon_0. E ~~~~~~~~(2)\]
Avec
- \(\varepsilon_0=8,85.10^{-12}~ \frac{V.s}{A.m}\) permittivité du vide,
- \(\varepsilon_r\) permittivité relative \(\varepsilon_r=1\) pour l'air et le vide.
Si un diélectrique est placé entre les plaques d'un condensateur à plaque, la capacité du condensateur est donnée par la relation suivante:
\[ C= \varepsilon_r. \varepsilon_0. \frac{S}{d} ~~~~~~~~(3)\]
Avec
- \(S\): La surface de la plaque,
- \(d\): l'écart de la plaque.
Travail expérimental
Montage
Le montage expérimental est illustré sur la fig. 2
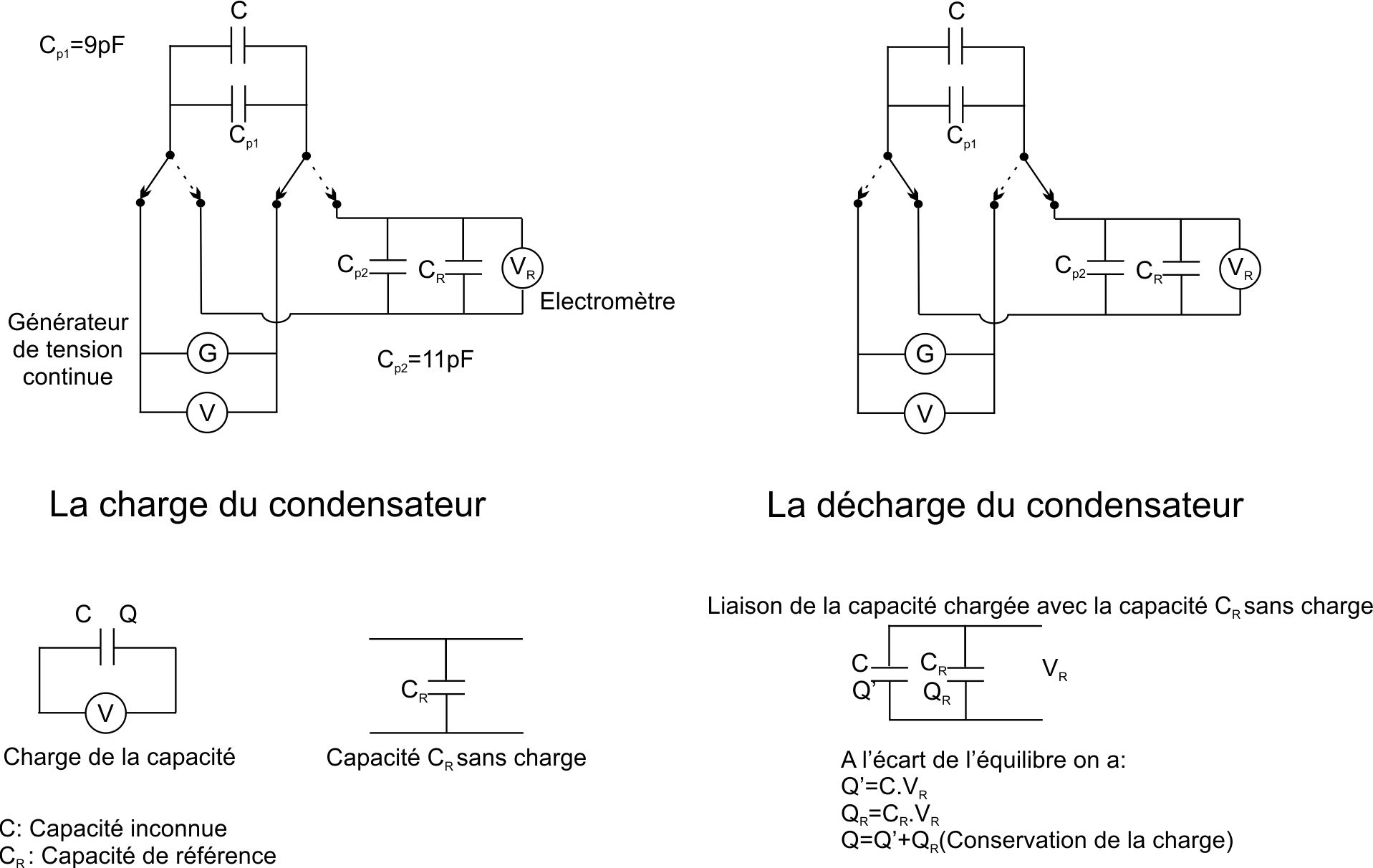
On a:
\[ C = \frac{Q}{V} \] \[ \Rightarrow Q =\frac{Q}{V}.V_R+C_R.V_R~\Rightarrow Q= \left( 1-\frac{V_R}{V} \right) = C_R.V_R \] \[ \Rightarrow Q =\frac{C_R.V_R}{1-\frac{V_R}{V}}=\frac{C_R.V_R}{\frac{V-V_R}{V_R}}=\frac{C_R.V_R}{V-V_R}.V \]donc
\[ Q = \frac{C_R.V_R}{V-V_R}.V \]Si \(V>> V_R\)
\[ Q = C_R.V_R \]donc
\[ C = C_R.\frac{V_R}{V} \]- Monter la paire de petites plaques (\(S=0,0531~m^2\)) et utiliser les entretoises pour régler une distance entre les plaques.
- Relier le pôle négatif de l'alimentation à la plaque de droite et à la masse de l'amplificateur électromètre.
- Relier le pôle positif de l'alimentation à la douille \(B\) du commutateur inverseur.
- Relier la douille \(A\) du commutateur inverseur à la plaque de gauche et la douille \(C\) à l'entrée de l'amplificateur électromètre.
- Enficher le condensateur de référence \(C_R = 228~ nF\) sur l'amplificateur électromètre et brancher le voltmètre à la sortie.
- Brancher le deuxième voltmètre pour la mesure de la tension \(V_R\) à la sortie de l'alimentation.
Mesure de la permittivité du vide
- Régler la tension V = 300 V.
- Utiliser les entretoises pour régler une distance entre les plaques \(d = 5~ mm\).
- Établir la liaison avec le commutateur inverseur et décharger le condensateur à plaques.
- Réduire successivement la distance entre les plaques avec un pas de \(0,5\), charger le condensateur et mesurer la tension pour chaque écartement des plaques.
Compléter le tableau de mesure suivant:
\( \begin{array}{|c|c|c|c|c|}
\hline
~~~~~d(mm) ~~~~~& ~~~~~\frac{1}{d} ~~~~~& ~~~~~\zeta=\frac{C_R. V_R}{V}~~~~~&~~~~~C=\zeta-C_{P2}~~~~~& ~~~~~\varepsilon_0=\frac{C.d}{S} ~~~~~\\
\hline \hline
1& & && \\ \hline
1,5 & & && \\\hline
& & && \\\hline
5 & & && \\
\hline
\end{array}
\)
- Tracé la courbe \(C=f(d)\).
- Tracé la courbe \(C=f(\frac{1}{d})\).
- Calculer la pente de la courbe \(C=f(\frac{1}{d})\).
- Déduire la valeur de la permittivité du vide \(\varepsilon_0\) et \( \Delta \varepsilon_0\).
Mesure de la permittivité relative d'une plaque de plastique (Radiographie)
- Placer la plaque plaque de plastique (Radiographie) entre les deux grandes plaques en veillant à ce que les plaques du condensateur soient bien en contact avec toute la surface de cette plaque de plastique.
- Régler la tension V = 300 V.
- Mesurer \(V_R\).
- Déduire la valeur de la permittivité relative \(\varepsilon_r\) et \( \Delta \varepsilon_r\).
