TP Physique1

I. Goals :

- Highlight the movement of an elementary mechanical system: the oscillating pendulum.

- Determine the spring stiffness constant by two methods: static and dynamic.

- Measure the value of an unknown mass from the spring calibration curve.

II. USED MATERIAL :

• A support.
• A metal rod.
• A spring of negligible mass
• A box of marked masses.
• A graduated ruler.
• A stopwatch.
• A mass of unknown value.
  
• 
  

III. THEORY :

     III.1. Static study:

When a mass m is suspended from a spring, the latter lengthens and exerts a force F   on the object responsible for its elongation; this force is called spring tension.

The elongation of the spring is noted x_eq and is defined by:

 

       where   l₀   : is the empty length of the spring

                      l    :  the length of the extended spring.  

A stiffness spring k  , whose mass will be neglected, is suspended vertically by its upper end from a support.

By applying Newton's first law, we have :

 At Equilibrium  :


From where, by projection on the axis of movement oriented vertically, we obtain:

 III.2. Dynamic study :

Using the previous spring, in addition to its first elongation Δl₀ = x_eq due to the clinging mass, we stretch the spring with a distance x (see Fig 2).

By applying Newton's second law, we have :  


By projection on the axis of movement oriented vertically, we get :  p_x - F_x = a_x

Using the relations :  

Using the relation (1), we obtain the differential equation of the oscillatory movement.

We can thus determine the expression of the period of the pendulum:

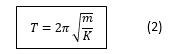
Physically, the period   represents the time of one oscillation.

IV. expErimental PROCEDURE:

IV.1. Static study:

1. Start by hanging the spring from the horizontal rod.

2. Attach the ruler so you can take precise measurements.

3. Measure the empty length l₀ of the spring.

4. Then you must first suspend the weight rack to be able to place the masses on it.

5. Different known masses (m ) of increasing values (see the table on the TP-sheet) are attached to the spring.

    At equilibrium, measure the corresponding elongations (X = x_eq ), taking into account the mass of the weight rack.

   For each mass, take a minimum of three measurements (each student will take one measurement).

    Record your results in the table.

6. To preserve the spring, you must unhook the mass directly after performing the measurement.

    Never leave masses attached to the spring!!

7. On a millimeter sheet, draw the calibration curve of the spring   X = f(m). 

 IV.2. Determination of the unknown mass of a body :

We want to determine the unknown mass m of a body from the calibration curve of the spring, for this :

1. Take the device used previously and put the unknown mass to the spring.

2. Measure the elongation X of the spring.

3. Use the spring calibration curve to determine the value of the mass m.

IV.3.Dynamic study :

1. Resume the previous device. Attach a known mass m to the spring.  

2. Stretch the spring (taking it away from its equilibrium position) a small distance, perfectly vertically, then let go of the mass without initial velocity.

3. Let the mass oscillate and measure the period of the oscillations T (read and carefully follow the measurement instructions on the sheet hung in the laboratory).

4. For each mass, take a minimum of three measurements (Each student will take one measurement).

5. Change mass and follow the same steps. Fill in the measurement table on the TP-sheet.

6. On a millimeter sheet, draw the calibration curve of the spring  T² = f(m).