Numpy et Matplotlib
Exercice 1 :
Une balle est lancée vers le haut avec une vitesse initiale \(v_0 = 5 m/s\) et une hauteur initiale \(y_0 =3m\).
- Tracer y(t) et v(t) dans la même figure à partir de t = 0 jusqu'à ce que la balle touche le sol.
Exercice 2 :
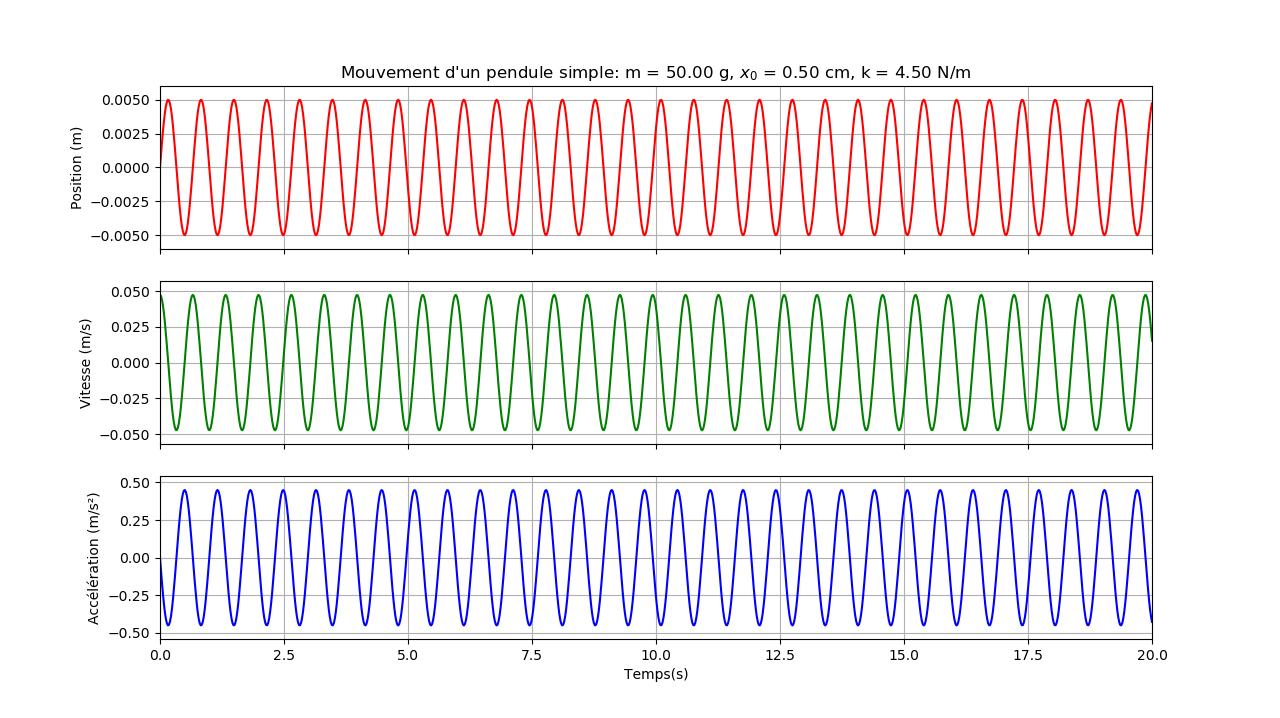
Une masse \(m = 50 g\) est accrochée à un ressort avec une constante de raideur \(k = 4 N/m\). On écarte la masse d'une petite distance \(x_0 = 0.5 cm\).
- Tracer la position, la vitesse et l'accélération de la masse en fonction du temps.
- Tracer la trajectoire dans l'espace des phases: l'axe horizontal représente la position et l'axe vertical celui de la vitesse.
- Etudier les cas pour \(k = [0.5, 1, 2, 4, 6, 8] N/m\)
La solution de la question 2 est de la forme:
Exercice 3 :
Considérons la fonction d'énergie décrivant un pendule simple donnée par:
\( E(x, v) = \frac{v^2}{2}-cos(x) \)
- Calculer E dans le domaine \( [-4 \pi, 4 \pi] \times [-2 \pi, 2 \pi] \)
- Créer un contour ou un tracé de contour rempli en utilisant respectivement plt.contour(E) ou plt.contourf(E).
- Tracer la courbe \(E(x, v)\), courbe à 3 dimensions sur l'axe des \(x\) la position, sur l'axe des \(y\) la vitesse et sur l'axe des \(z\) l'énergie
Astuce: utiliser numpy.meshgrid
Modifié le: mardi 14 juillet 2020, 06:27
