Élasticité d’un solide, Pendule et appareil de torsion
L'objectif de ce TP est d'effectuer une étude expérimentale pour déterminer la valeur du module de Young de fils métalliques de natures, et caractéristiques dimensionnelles différentes à travers la mesure
de leur constante de torsion \( C \). Pour cela, on utilisera une méthode statique et une méthode dynamique. on s'attachera bien sûr à comparer les résultats des deux méthodes.
Dispositif expérimental
- Dispositif de torsion
- Chronomètre
- 2 masses de 200 g chacune
- 1 dynamomètre,
- Fils de Torsion.
Étude Théorique
Les corps solides se déforment lorsqu'ils sont soumis à des forces. Dans un corps non déformé, la configuration des molécules correspond à l'état de son équilibre thermique; toutes ses parties étant par ailleurs, en équilibre mécanique. Si le corps est déformé, la position des molécules varie; le corps sort de son état d'équilibre et des forces, dite contraintes internes, y prennent naissance et tendent à le ramener à son état d'équilibre.
Étude statique
Soit un fil mince rectiligne d'axe \( OO' \), de section circulaire de rayon \( R \) et de longueur L. La section passant par O est maintenue fixe. Un couple de moment M parallèle à l'axe vertical \( OO' \), est appliqué à l'autre section qui passe par \( O' \). La torsion est telle que les sections ne sont pas déformées. Elles subissent une rotation d'amplitude proportionnelle à leur distance relativement à la section fixe passant par \( O \).
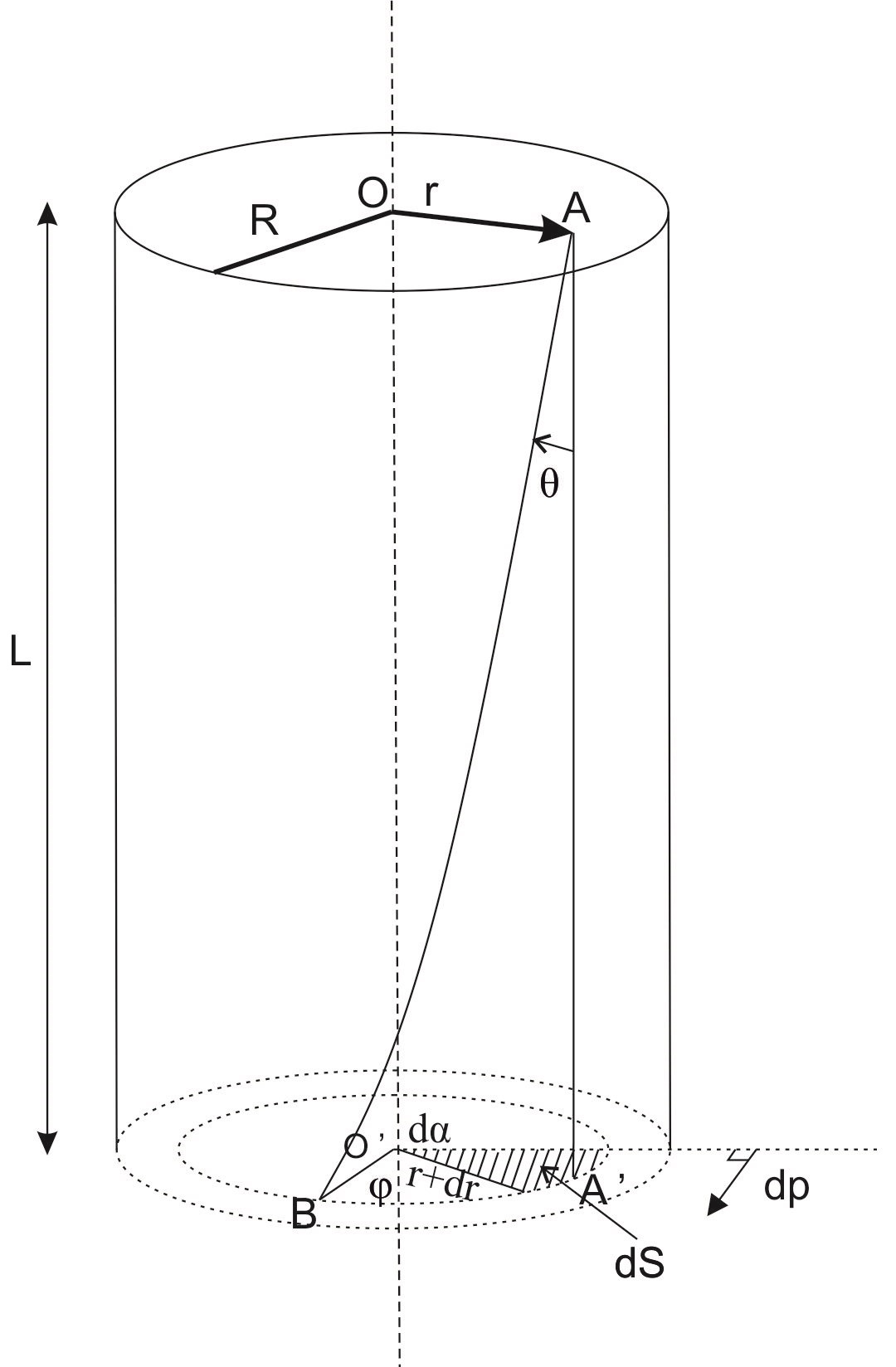
Tous les points de la section inférieure passant par \( O' \) tournent alors d'un petit angle \( \varphi\). Soit \( dS \) un élément de cette section. Cet élément se trouve au point \( A' \)avant la torsion et au point B après la torsion tel que \( OA'=OB=r \).
La verticale \( AA' \) passera à la position \( AB \). Le corps subira une déformation de glissement d'un angle \( \theta \)tel que:
\[\theta=\frac {\widehat{A'B}}{L} =\frac{r\varphi}{L}~~~~~~~~(1)\]Nous savons d'autre part que, pour faire glisser un élément de surface \( dS \) d'un angle \( \Theta \), il faut appliquer une force égale à:
\[dp=\mu \theta dS ~~~~~~~~(2)\]μ est le module de glissement de ce corps. L'élément de surface dS S'écrit:
\[dS=r dr d\alpha ~~~~~~~~(3)\]En remplaçant les expression de \( \Theta \) et de \( dS \) dans l'équation 2, nous obtenons:
\[dp=\frac{\mu r^2 \varphi}{L} dr d\alpha ~~~~~~~~(4)\]Le moment de cette force, par rapport à l'axe \( OO' \), s'écrit:
\[d\vec{M}= \vec{r}\wedge d\vec{p}~~~~~~~~(5)\]Avec \(\vec{r}\) perpendiculaire à \(d\vec{p}\), l'équation 3 devient:
\[d\vec{M}= \frac{\mu r^3 \varphi}{L} d\vec{r} d\alpha ~~~~~~~~(6)\]Le moment total agissant sur la section droite inférieure, passant par \( O' \), vaut alors:
\[M=\int_{r=0}^{R} \int_{\alpha=0}^{2\pi} \frac{\mu r^3 \varphi}{L} dr d {\alpha}~~~~~~~~(7)\] \[M= \frac{\mu \pi R^4 \varphi}{2 L}~~~~~~~~(8)\]En notant d le diamètre du fil étudié (d=2R), l'équation 8 devient:
\[M= \frac{\mu \pi d^4}{32 L}~~~~~~~~(9)\]D'autre part, nous savons que, dans le domaine de l'élasticité du matériau utilisé, le moment du couple appliqué en un point \( D \) est proportionnel à l'angle \( \varphi \):
\[M= C \varphi~~~~~~~~(10)\]La constante de proportionnalité \( C \) est appelée constante de rigidité ou de torsion du matériau considéré Nous déduisons à partir des équation 9 et 10 que:
\[M= C \varphi= \frac{G \pi d^4 \varphi}{32 L}~~~~~~~~(11)\]d'où:
\[C= \frac{G \pi d^4 }{32 L}~~~~~~~~(12)\]Étude dynamique
La section droite supérieure (Passant par le point \( O \)) du fil étant encastrée (fixe), nous fixons à l'autre section droite (Passant par \( O' \)) un système constitué d'une tige en bois horizontale sur laquelle peuvent se fixer 2 masselottes (\( m \)) placées systématiquement par rapport à l'axe vertical \( OO' \)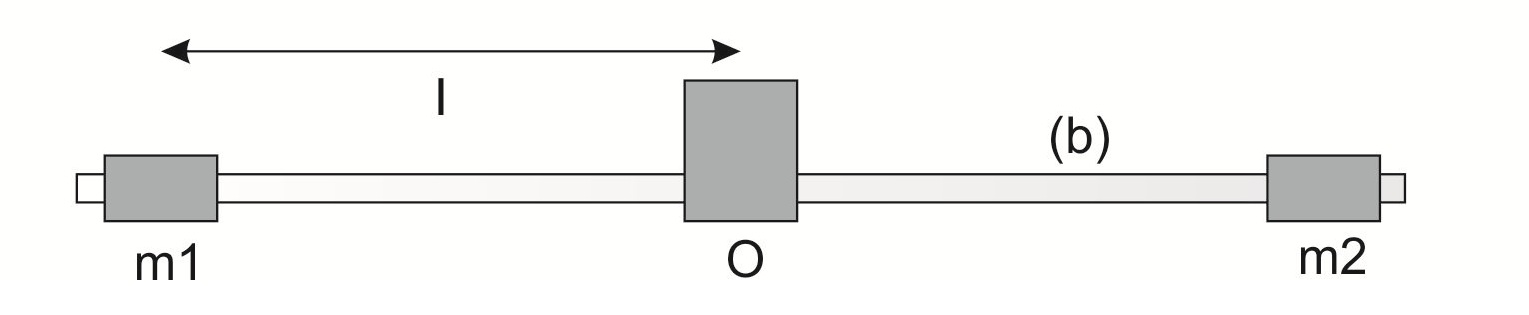
Figure 2: Pendule de torsion
En appliquant la relation fondamentale de la dynamique de rotation de système, constitué de la tige et des masselottes, nous obtenons l'équation différentielle suivante:
\[M_{/OO'}=-C\varphi= I_{/OO'}\left( \frac{d^2\varphi}{dt^2}\right)~~~~~~~~(13)\]Où (-Cφ) est le moment exercé par le fil tordu d'un angle φ sur le système (tige + masselottes): c'est un moment de rappel.
\[I_{/OO'}\] est le moment de rappel d'inertie du système par rapport à l'axe OO'. La solution de l'équation différentielle (13) donne l'équation du mouvement sinusoïdal de rotation de période: \[T= 2\pi\left( \frac{I_{/OO'}}{C}\right) ^{1/2}~~~~~~~~(14)\]Dans cette dernière équation, \(I_{/OO'}\) est la somme des moments d'inertie des masselottes \(I_{m/OO'}\) et de la tige \(I_{t/OO'}\):
\[I_{/OO'}= I_{m/OO'}+ I_{t/OO'}~~~~~~~~(15)\]Dans le cadre de cette manipulation, on négligera le moment d'inertie de la tige devant celui des masselottes:
\[I_{/OO'}\approx I_{m/OO'}=2ml^2~~~~~~~~(16)\]L'expression de la période de oscillations T est alors donnée en fonction de la constante de torsion par:
\[T= 2\pi\left( \frac{2ml^2}{C}\right) ^{1/2} ~~~~~~~~(17)\]caractérisation du matériau utilisé
En théorie, la constante de torsion \( C \) d'un fil cylindrique se calcule par :
\[C=\frac{\pi}{2}\frac{R^4}{L} G ~~~~~~~~(18)\]Où G le module d'élasticité transversale ou module de Coulomb. Le module de Coulomb est une caractéristique propre à chaque matériau. il s'exprime en \(N.m^{-2}\) et se calcule par:
\[G= \frac{E}{2(1+\nu)}~~~~~~~~(19)\]Où E est le module de Young du matériau, et ν est le coefficient de Poisson.
\[ \begin{array}{|l|c|c|} \hline ~~~~~~Matériau ~~~~~~&~~~~~~ E ~ en ~ Mpa ~~~~~~&~~~~~~\nu ~~~~~~\\ \hline \hline Acier&210000&0.30\\ Acier ~ inox 18-8&189000&0.30\\ Aluminium&70000&0.33\\ Argent&70000&0.37\\ cadmium &70000&0.44\\ Chrome&252000&0.30\\ Cuivre&112000&0.34\\ Fer&210000&0.30\\ Fonte&126000&0.25\\ Laiton&112000&0.33\\ Magnésium&42000&0.25\\ Molybdène&329000&0.31\\ Monel&17000&0.28\\ Nickel&21000&0.41\\ Or&70000&0.42\\ Plomb&15400&0.41\\ Platine&168000&0.39\\ Titane&11000&0.34\\ Tungstène&357000&0.19\\ Zinc&91000&0.28\\ Verre&46200&0.24\\ Caoutchouc&1500&0.50\\ Acétal&2800&0.35\\ Plexiglas&3160&0.40\\ Polycarbonate&2320&0.38\\ Téflon&400&0.48\\ Nylon&1100&0.34\\ Polyéthylène&760&0.46\\ \hline \end{array} \]
Tableau 1: Caractéristiques de quelques matériaux
Travail expérimental
Remarque concernant la manipulation
- En réalisant le montage, faite attention à ce que le fil du matériau à caractériser soit le plus droit possible et parallèle au support rigide du pendule. De plus, il faut que le fil soit bien fixé (serrez bien le vis concernée).
- En utilisant le dynamomètre, vous remarqu erez que celui-ci est relativement imprécis dans ses toutes première graduations. Pour palier à cela, évitez dans vos mesures les petites valeurs de forces.
- Nous rappelons, que dans cette manipulation, le calcul d'erreur tient une place importante et que cela doit se refléter non seulement dans vos résultats mais surtout dans le tracé de vos courbes et, plus forte raison, pour les paramètres que vous tirerez de celles-ci.
Étude statique
- Placer le fil d'aluminium de \(L=500mm\) et \(d=2mm\) bien verticalement
- A l'aide de la vis située sous le cadran, ajuster sa position pour lire \(\varphi_{réf}=0\)
- Faire passer la boucle d'un dynamomètre dans une des pointes de la barre.
- Tirer sur le dynamomètre de la qualité voulue en le maintenant perpendiculairement à (b) pour écarter la barre de sa position d'équilibre et relever l'angle obtenu,
Les intensités des forces à utiliser sont laissées à votre appréciation. Attention cependant à ne pas trop déformer les fils pour ne pas les endommager.
Les angles sont mesurés en degrés mais doivent être exprimés en radians pour les calculs; de même, les masse sont à convertir en \(Kg\) et les distance en \(m\) avant de faire les calculs.
- Tracé la courbe \(M=f(\varphi)\).
- Calculer la constante de torsion C pour cette expérience.
- Déduire la valeur du module de Young pour ce matériau.
- Comparer les résultats théorique et pratique du module de Young
Étude dynamique
Isochronisme des oscillations
Les oscillations sont dites "isochrones" si leur période T ne dépend pas de la déviation initiale imposée au système.
Écarter (b) de sa position d'équilibre d'un angle φ à noter, déclencher le chronomètre au moment de lâcher (b) sans vitesse initial et mesurer la durée t que met ce pendule pour décrire \(10\) périodes. Effectuer la même mesure \(3\) fois.
Reprendre les mêmes mesures en changeant la position de départ du pendule.
Compléter le tableau de mesure suivant:
\[ \begin{array}{|c|c|c|c|} \hline ~~~~~~~~t ~~~~~~~~& ~~~~~~~~\Delta \varphi= 20^\circ ~~~~~~~~& ~~~~~~~~\Delta \varphi= 30^\circ ~~~~~~~~& ~~~~~~~~\Delta \varphi= 40^\circ~~~~~~~~\\ \hline \hline t_1 [s]& & & \\ \hline t_2 [s] & & & \\ \hline t_3 [s] & & & \\ \hline t~moyen [s] & & & \\ \hline \end{array} \]- Calculer la période d'oscillation moyenne T et ΔT.
- Calculer la constante de torsion C' pour cette expérience, ainsi la valeur de G.
- Déduire la valeur du module de Young et la comparer avec la valeur obtenue par la méthode statique et conclure.
Étude de l'influence de la géométrie du fil sur la constante de torsion
On souhaite à présent étudier le comportement de l'Aluminium en utilisant des fils de différentes longueurs et différents diamètres réalisés dans ce même métal.
Pour cela on utilisera la méthode dynamique. On reprendra donc la méthode précédente, en positionnant les masses au même endroit.
- Compléter le tableau suivant.
- Interpréter et conclure.

