L'objectif de ce TP est de se familiariser avec les différents systèmes, ainsi que l'étude des empilements et la notion des composés chimiques les plus courants.

Étude Théorique

Réseaux de Bravais

Définitions

• Un réseau est une abstraction mathématique. Un réseau est formé de nœuds de sorte que pour remonter à la structure, on associe à chaque nœud une base (motif).
• Un motif (ou base) est l'atome ou groupement d'atomes constituant l'unité structurale affectée à un nœud du réseau. Cette base doit être identique en composition, orientation et position des atomes de sorte qu'une structure peut être décomposée en un réseau plus le motif.
• La maille conventionnelle est une maille qui appartient à l'un des 14 réseaux de Bravais.
• La maille élémentaire est la plus petite maille que l'on peut obtenir. Une maille élémentaire contient un seul nœud. Le nombre d'atomes d'une maille élémentaire est donné par le nombre d'atomes dans la base. Si la maille conventionnelle contient le nombre \( N \) de nœuds:
  • à \( N \) nœuds correspond le volume \( V \)de la maille conventionnelle;
  • à \( 1 \) nœud correspond le volume \( V_e \) de la maille élémentaire.

  Le volume de la maille élémentaire est donné par: 

\( V_e= \frac{V}{N} \)          (1)

• La multiplicité c'est le nombre de sphères appartenant à la maille élémentaire, on a besoin de savoir combien de sphères appartiennent réellement à chaque maille pour pouvoir les dénombrer exactement, et faire les calculs de masse, de densité ...
  

• La compacité c'est le rapport du volume réellement occupé sur le volume total:




\( C=\frac{V_{occupé~par ~les~ shères}}{V_{total~de~la~maille}} \)          (2)


La compacité est donc toujours comprise entre \( 0 \) et \( 1 \)


• La Coordinence dans un réseau, un atome (ou ion), \( A_i\) donnée est entouré d'autres atomes (ou ions)\( A_j\), pas forcément identiques, et éloignés à des distances inter atomiques variables. La coordinence de l'atome \( A_i\) est le nombre \(x \) de ses atomes plus proches voisins \( V \)
• Taux de remplissage d'un réseau On appelle taux de remplissage le rapport du volume occupé par les sphères au volume total.




\( \tau = N\frac{V_s}{V} \)          (3)


\( N \) étant le nombre de sphères dans la maille, \( V_s\) le volume d'une sphère égal à \( \frac{4}{3}\pi R^3\) ; \( R \)étant le rayon de la sphère et \( V\) le volume de la maille.

Réseaux de Bravais bidimensionnels

\[ \begin{array}{|l|l|l|} \hline ~~~~~~Système~~~~~~&~~~~~~Réseaux~~~~~~&~~~Nature~de~la maille~~~\\\hline Oblique &1: P& a_1\neq a_2 ~~~\Phi \neq 90^\circ \\ Carré &1: P& a_1 = a_2 ~~~\Phi = 90^\circ \\ Hexagonal &1: P& a_1= a_2 ~~~\Phi = 120^\circ \\ Rectangulaire&2: P& a_1\neq a_2 ~~~\Phi = 90^\circ \\ \hline \end{array} \] 

Réseaux de Bravais tridimensionnels

A trois dimensions, il existe 14 réseaux de Bravais. Un réseau est défini par les vecteurs \( \vec{a_1}, \vec{b_2}\)  et \( \vec{c_3}\) , notés parfois aussi, \( \vec{a}, \vec{b}\)  et \( \vec{c}\), et les angles \( \alpha, \beta\)  et \( \gamma\) tels que: \( \alpha= \vec{a_2}, \vec{a_3} \), \( \beta= \vec{a_3}, \vec{a_1} \) et \( \beta= \vec{a_1}, \vec{a_2}\) Les quatorze types de réseaux de Bravais peuvent être groupés en sept systèmes d'après les sept types conventionnels de mailles: triclinique, monoclinique, orthorhombique, tétragonal, cubique, trigonal et hexagonal.

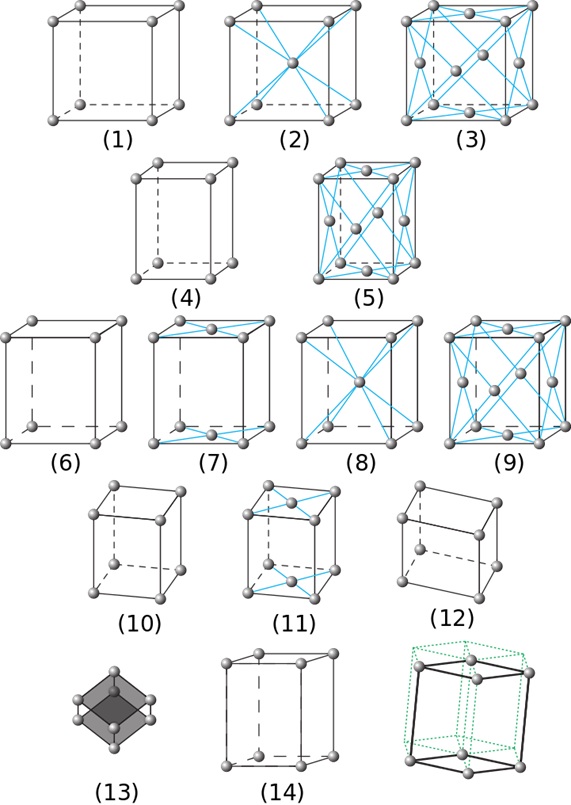
Sur la figure 1 sont représentés les 14 réseaux de Bravais, les mailles figurées sont les mailles conventionnelles qui ne sont pas toujours primitives ou élémentaires.

La distinction entre les différents systèmes se fait en donnant les relations qui lient les vecteurs. Les mailles représentées dans le tableau ci-dessous sont des mailles conventionnelles. Les notations sont P: primitif, I: corps centré (I de l'allemand Innenzentrierte), F: faces centrées et C: bases centrées.

\( \begin{array}{|l|l|l|} \hline ~~~~~~Système~~~~~~&~~~~~~Réseaux~~~~~~&~~~Nature~de~la~ maille~~~\\ \hline Cubique &3 : P-I-F & a_1 = a_2 = a_3 ~;\alpha=\beta=\gamma=90^\circ \\ Quadratique - Tétragonal &2 : P-I & a_1 = a_2 \neq a_3 ~;\alpha=\beta=\gamma=90^\circ \\ Orthorhombique &4 : P-C-I-F & a_1 \neq a_2 \neq a_3~~;\alpha=\beta=\gamma=90^\circ \\ Monoclinique &2 : P-C & a_1 \neq a_2 \neq a_3~~;\alpha=\gamma=90^\circ \neq \beta \\ Triclinique &1 : P & a_1 \neq a_2 \neq a_3~~;\alpha \neq \beta \neq \gamma \\ Rhomboédrique ou Trigonal &1 : P & a_1 = a_2 = a_3~~;\alpha=\beta=\gamma\neq 90^\circ <120^\circ \\ Hexagonal ou triangulaire &1 : P & a_1 = a_2 \neq a_3~~;\alpha=\beta=90^\circ, \gamma=120^\circ \\ \hline \end{array} \)

• Dans le système Cubique, on trouve trois réseaux: le réseau cubique simple (P) dont la maille est élémentaire, le réseau cubique centré (I) et le réseau cubique à faces centrées (F).
• Dans le système Tétragonal ou Quadratique, la maille la plus simple est un prisme à base carrée; cette maille est élémentaire. Un autre type existe avec une maille centrée (I).
• Dans le système Orthorhombique, il y a quatre types réticulaires: un réseau dont la maille est élémentaire (P), un réseau à base centrée (C), un réseau centré; et un à faces centrées (F).
• Dans le système Monoclinique, on trouve deux types réticulaires, l'un dont la maille est élémentaire (P) et un autre dont la maille est conventionnelle, elle peut être à bases centrées (C) ayant alors des nœuds au centre des rectangles du plan.
• Dans le système Triclinique, on trouve un seul type réticulaire avec une maille élémentaire (P) dont les 3 vecteurs et les 3 angles ont des mesures différentes.
• Dans le système Trigonal ou Rhomboédrique, on choisit généralement un rhomboèdre comme maille. C'est une maille élémentaire.
• Dans le système Hexagonal ou triangulaire empilés, la maille conventionnelle est un prisme droit dont la base est un losange d'angle \(60^\circ\). Ce réseau est simple et la maille est élémentaire.

Empilements

On considère les atomes comme des sphères dures indéformables de rayon \( R \).

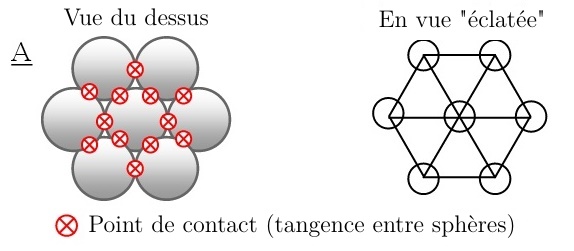
Dans un plan \( A \) l'empilement le plus compact possible est obtenu lorsque les sphères sont tangentes. Leurs centres forment des triangles équilatéraux de coté \(a=2R\) . Une sphère a alors\( 6 \) voisins.

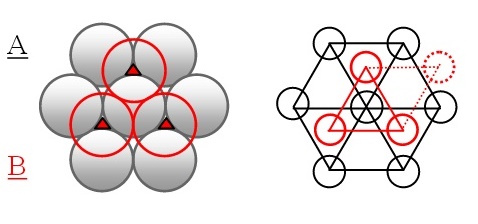
Au-dessus du plans \(A\) une seule solution possible, plan \(B\), dans lequel chaque sphère \(B\) est au contact de 3 sphères du plan \(A\). Les sphères \(B\) sont localisées à la verticale des barycentres des triangles équilatéraux qui décrivent le plan \(A\).

Les sites tétraédriques et octaédriques

Le site tétraédrique

Si l'on superpose à la première couche A une deuxième couche B de sphères identiques, chaque sphère du plan supérieur B repose sur trois sphères du plan inférieur A, de façon à obtenir le système le plus compact possible. Ces quatre sphères forment les sommets d'un tétraèdre régulier de côté \(2R\) et délimitent une lacune appelée site tétraédrique. Réciproquement chaque sphère du plan inférieur est en contact avec trois sphères du plan supérieur.

Si nous considérons 3 plans d'atomes (1) (2) et (3), un atome du plan médian (2) et ses proches voisins dans les plans (1) et (3): il est en contact avec trois atomes du plan supérieur (1) et trois atomes du plan inférieur (3).

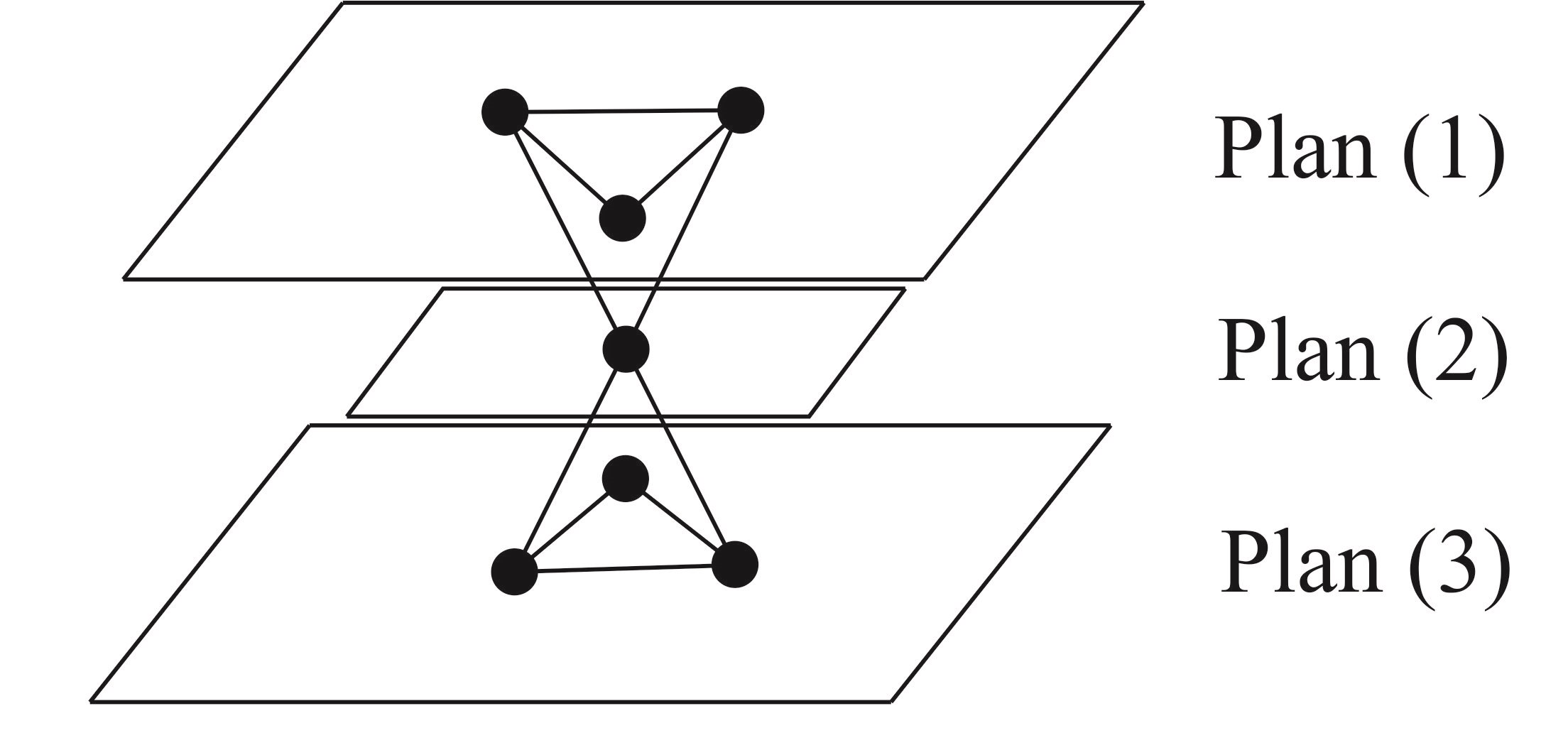
Les atomes du plan (1) et (2) forment un site tétraédrique. Ceux des plans (2) et (3) forment un autre site tétraédrique. À chaque atome correspondent donc 2 sites tétraédriques. Si \(N\) est le nombre d'atomes appartenant au cristal, il y aura \(2N\) sites tétraédriques.

Le site octaédrique

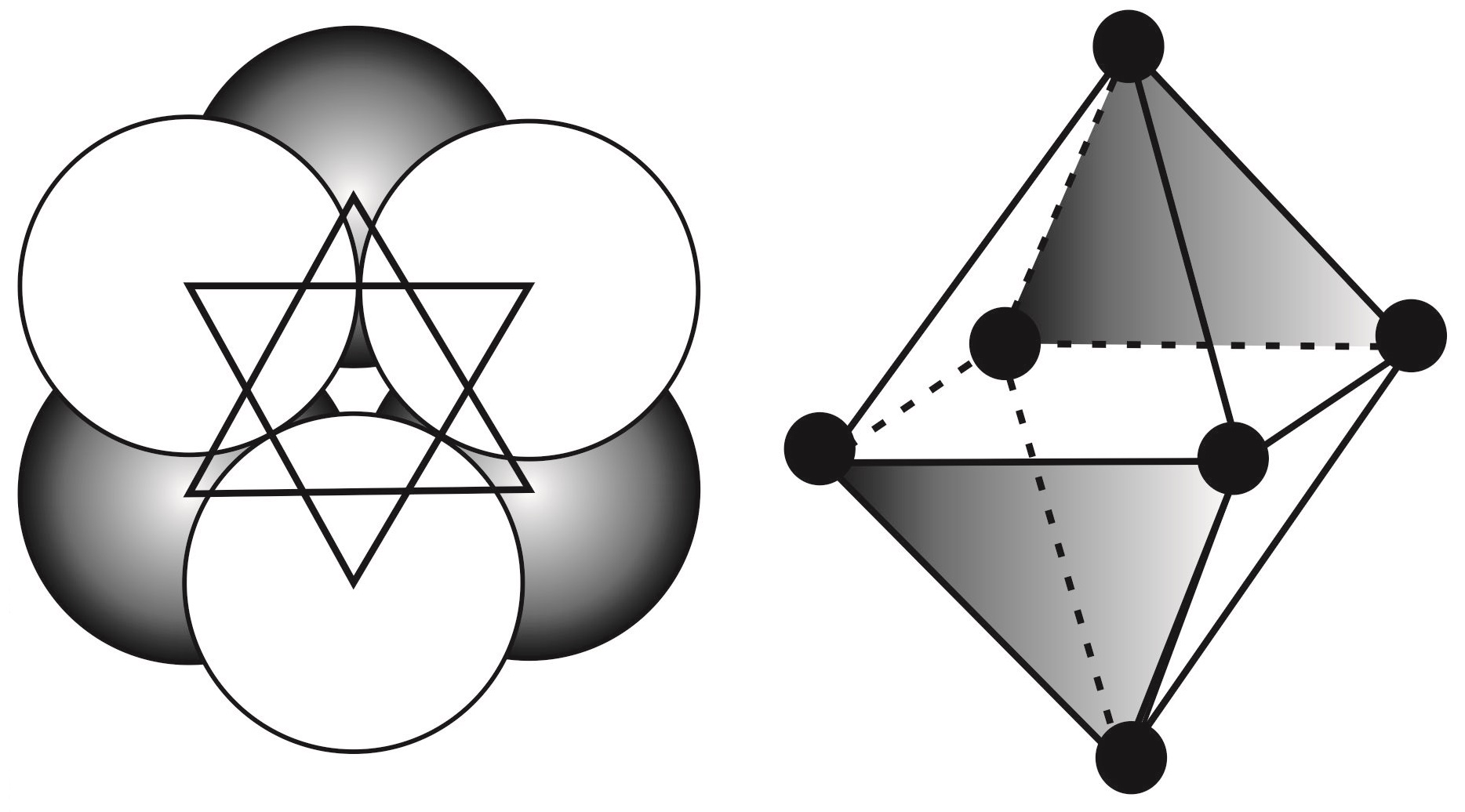
Ce mode d'assemblage entraîne aussi l'existence de sites octaédriques délimités par six sphères appartenant à deux plans successifs: trois atomes du plan inférieur dont les centres constituent les sommets d'un triangle équilatéral et trois atomes du plan supérieur dont les centres forment les sommets d'un triangle équilatéral opposé au premier.

L'ensemble des centres des six atomes sont les sommets d'un octaèdre régulier de côté \(2R\). Il y a \(N\) sites octaédriques pour \(N\) atomes.

Travail expérimental

Empilement bidimensionnels

1. À l'aide de tiges en bois de longueur différente réaliser les différents réseaux de Bravais bidimensionnels.
2. Pour réaliser des empilements, placer les disques pour former une première couche de la façon la plus compacte possible. On obtient les deux arrangements donnés dans les figures suivantes:

Donner le nombre de premiers proches voisins ainsi que leur distance en fonction de R sous forme de tableau:

\( \begin{array}[h]{|c|c|c|} \hline ~~~~~~Arrangement~~~~~~&~~~~~~1^{er} ~proches ~voisins~~~~~~&~~~Distance~~~\\ \hline A&&\\ \hline B&&\\ \hline \end{array} \)

• Donner le réseau de Bravais à 2 dimensions en précisant ses paramètres.
• Déterminer le nombre de billes par maille.

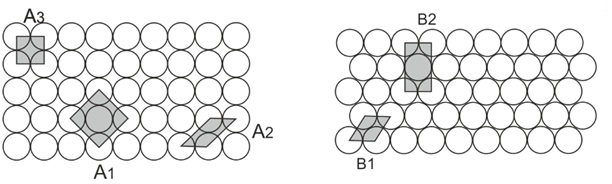
Consigner tous les résultats obtenus dans un tableau :

\( \begin{array}[h]{|c|c|c|} \hline ~~~~~~~~~~~~&~~~~~~Nom~et ~~~~~~&~~~Nombre ~~~\\ ~~~~~~Maille~~~~~~&~~~~~~paramètres~de ~~~~~~&~~~ de ~billes~~~\\ ~~~~~~~~~~~~&~~~~~~ maille~~~~~~&~~~par ~maille~~~\\\hline A1&&\\ A2&&\\ A3&&\\ B1&&\\ B2&&\\ \hline \end{array} \)

Empilement tridimensionnels

1. Toujours à l'aide de ces tiges en bois de réaliser les différents réseaux de Bravais tridimensionnels, Cubique, tétragonal, orthorhombique et monoclinique.
2. Sur chaque trame, empiler successivement 4 couches. Montrer que sur la trame (b) il existe 2 manières d'obtenir un empilement compact. Décrire en détail les 3 empilements obtenus. Faire des dessins.
3. Représenter par un schéma clair (forme éclatée) les 3 mailles basées sur A3 et B1 en indiquant successivement d'une couleur chaque couche empilée.
4. Déterminer le nombre d'atomes pour chaque maille, le paramètre de la maille en fonction de R ainsi que la compacité.

Notion de site

Considérons maintenant une structure \(Na Cl\) , designer soigneusement la maille, sachant que les ions \(Cl^-\) occupent le réseau \(cfc\) et les ions \(Na^+\) occupent les sites octaédrique. Déterminer:

• le nombre d'ions par maille,
• La coordinence,
• La compacité de la maille.