PW4: FREE FALL AND TWO-DIMENSIONAL BALLISTIC MOTION
FIRST PART: FREE FALL
I. GOALS :
- The study of the motion of a ball dropped without initial velocity in the gravitational field.
- The experimental determination of the acceleration of gravity g.
- Study of the effect of the mass on the value of the acceleration g.
II. USED MATERIAL :
- Two balls of different masses.
- A vertical rod which supports at its upper end an horizontal arm.
- An electronic counter.
- A ruler graduated in millimeters.
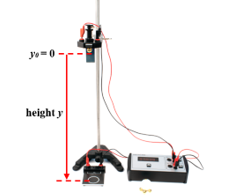
III. THEORY :
The relationship of distance versus time and the initial velocity of a body in free fall motion is given by the relation :
![]()
If we fix the origin of the heights at the starting
point of the body in free fall, i.e. h0 = 0 (figure above)
with zero initial velocity v0 = 0
, the previous
relation can be written in the form :
![]()
IV. EXPERIMENTAL PROCEDURE :
1. There is a vertical rod which supports at its upper end an horizontal arm.
2. At the free end of the horizontal arm, a mass m is held by a trigger between the tip and the slide by which it triggers a mechanical contact.
3. As soon as the mass is released with the trigger, the mechanical contact is cut and the electronic counter starts up.
4. The mass falls in free fall on the plate which will stop the counter. This system then allows us to measure the time t that the mass takes to travel a vertical distance h.
5. The experimental work consists in measuring the time t for several vertical distances h. The time t is taken using a digital meter.
6. For the measurement of h, use a ruler graduated in millimeters.
IV.1. Experience 1 : Follow the experimental procedure described above, using the ground metal ball m1. Fill in the table found in the technical sheet.
IV.2. Experience 2 : Repeat the previous experiment using the mass plastic ball m2.
Remarks : -The distance h is measured between the lower end of the ball and the plate.
To have good measurements and for the same height, take the average of
at least two time measurements.
SECOND PART : TWO-DIMENSIONAL BALLISTIC MOTION
I. GOALS :
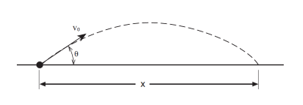
- The examination of the effect of the firing angle on the range.
- The determination of the initial velocity of a parabolic falling projectile.
II. USED MATERIAL :
- Mini launcher
- Stainless metal ball
- Carbon paper
- White paper
- Decameter

![]()

In the vertical direction, where the force of gravity applies, the vertical position y(t) is expressed by :
![]()
By taking y0 = 0, the point of fall, corresponding to the
return of the projectile to the initial vertical position, will be
:
![]()
Two solutions
exist :
![]()
The first solution corresponds to
the initial position and the second solution thus determines the range. By
introducing
in the equation of the horizontal position, we
obtain : 1. Choose on the device
(mini-launcher) the same release point (to have the same initial speed) and
this by placing the ball in the mini-launcher. Place it in the third position
indicated on the device One click corresponds to the 1st position,
two clicks to the 2nd position and three clicks to the 3rd
position. 2. Adjust the angle of the mini
launcher to zero degrees (0°) as well as the height of the mini-launcher. The opening
of the mini launcher must be at the same level as the table. 3. Place on the table a white sheet
above which we will place a 2nd sheet of carbon paper. This allows
you to leave a mark when the ball hits the table. 4. Change the shooting angles and
measure the range using the decameter. Theoretical
question :
Are there two
different launch angles giving the same range? 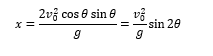
IV. EXPERIMENTAL PROCEDURE :
