TP Physique1

I. GOALS :

- Highlight the movement of an elementary mechanical system: the simple pendulum.

- Study the influence of different parameters such as length and mass on the proper period of a simple pendulum.

- Visualize the oscillatory motion and calculate experimentally the value of the earth's acceleration.

 II. IMPORTANT :

•  The protractor must be properly fixed to the horizontal rod to minimize errors on the angle.
•  The ruler must be fixed to a nut and using the brackets located on the ruler, the length of the wire can be measured without too much difficulty.
• Reading on graduated devices such as the ruler or the protractor must be done perpendicular to the device.
•  It must be ensured that the movement of the simple pendulum is indeed a swinging movement in a plane. There shouldn't be swings in all directions.

 III. USED MATERIEL :

•  An adjustable foot on which a rod is fixed horizontally.
•   Two balls, considered dimensionless, of masses  m₁  and   m₂  (  m₁ ≠ m₂).
• A graduated ruler of length  l=1m .
• An inextensible wire.

 IV.THEORY :

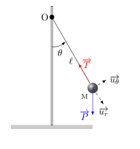
The simple pendulum is made by suspending a ball of mass  from an inextensible wire of length , attached to a bracket by its upper end. The ball is moved slightly away from its equilibrium position (amplitude  less than 10°) then released.

According to the figure opposite and by applying the fundamental principle of dynamics,

T, P, and m represent respectively the tension of the wire, the weight of the mass suspended on the wire and the acceleration of the pendulum.

By projecting onto the tangential axis oriented towards the unitary vector u_r,  we find the equation of motion :

θ^.., l and g represent respectively the angular acceleration of the pendulum, the length of the wire and the acceleration of earth's gravity.

Knowing that for low amplitudes, we have  sin θ ≈ θ, thus we obtain :

which can be written in the form :

with ω = g/l  and like T= 2π/ω  then we get the simple period formula :

V. EXPERIMENTAL PROCEDURE:

V-1. Influence of the length  of the wire on the period

In this part, we try to verify the influence of the length  of the wire on the period  of the movement. We start by suspending the ball  at the gallows, then, the length of the wire is varied. For each of the lengths considered, the ball is slightly moved away from its equilibrium position     then it is released without initial speed. Then, we measure the period  of the movement of the pendulum using the stopwatch. Finally, we draw l = f(t²)    on a millimeter paper.

V-2. Influence of the mass  of the pendulum on the period

In this part, we want to verify the influence of the mass of the ball on the period  of the movement. We replace the first mass ball  by a second mass ball  . We do the same measurements as for the first part then we draw the graph l = f(t²)  on a millimeter paper.