Diffraction of light waves
Purpose
The purpose of the lab experiment is as follows:
- To demonstrate the phenomenon of diffraction of light waves and to study the influence of various parameters on the diffraction pattern. Determining the conditions necessary for diffraction,
-
To demonstrate the phenomenon of interference of light waves.
Definition
Diffraction through a Narrow slit
Diffraction is the phenomenon in which a wave passing through a small aperture or encountering a small object changes direction without any alteration in frequency or wavelength. The significance of this phenomenon increases as the size of the obstacle or opening decreases.
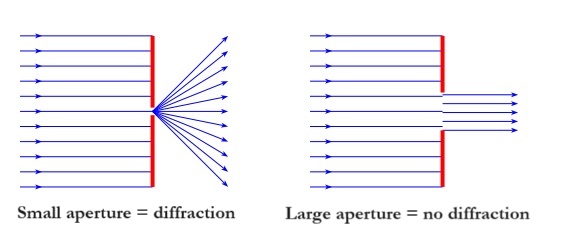
For the phenomenon of diffraction to occur, the size of the obstacle or aperture must be of the same order of magnitude as the wavelength of the wave.
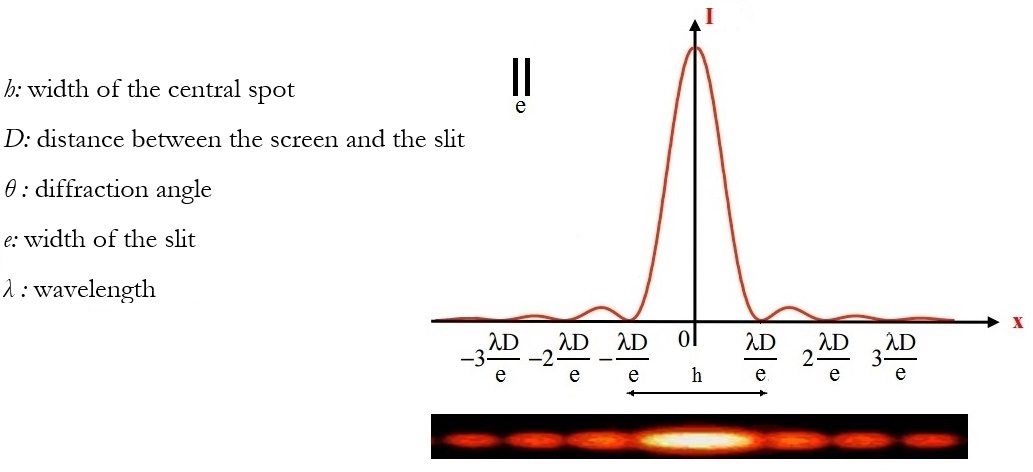
Consider diffraction caused by a narrow laser beam through a vertical slit with dimensions of the same order of magnitude as its wavelength. The beam diffracts, forming separate bright spots separated by dark regions known as extinctions. The central spot has a larger size and higher intensity than the others, with the size and intensity decreasing as one moves from the center toward the periphery.
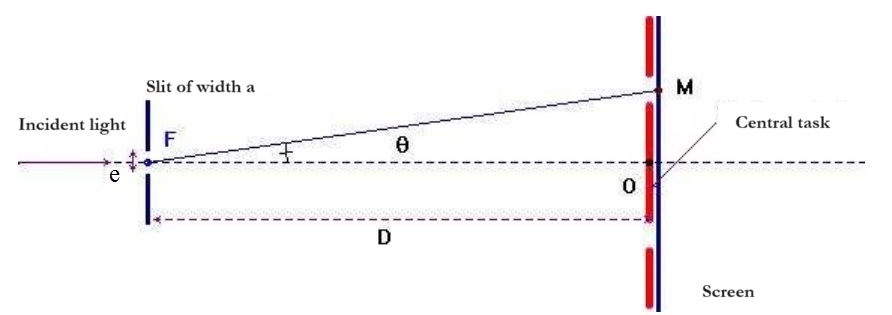
Under Fraunhofer conditions (which correspond to the diffraction of a plane wave at a great distance from the aperture or near the geometrical image of the light source), the intensity distribution is given by:
\( I(\theta)=I_0 \frac {sin^2 ~ \left( \frac{\pi e}{\lambda} sin ~ \theta \right) }{\left( \frac{\pi e}{\lambda} sin ~ \theta \right)^2 } \) (1)
Conditions for the minima:
\( I(\theta)=0 \) when\( \frac{\pi e}{\lambda} sin ~ \theta = \pm n \pi \) The first minimum is such that \( n=1 \)
But \( \theta \) petit \( \Rightarrow sin~\theta \approx \theta \approx tg \theta=\frac{x}{D} \) so:
\( h=\frac{2 \lambda D}{e} \) (2)
Where \( h = 2x \) is the width of the central spot.
Diffraction by two identical parallel slits
Light interference
The phenomena of interference result from the superposition of two light waves. They can only occur when the following conditions are met:
- The waves are coherent,
- They have the same frequency, hence the same wavelength,
- They are parallel,
- They have the same amplitude, or nearly the same.
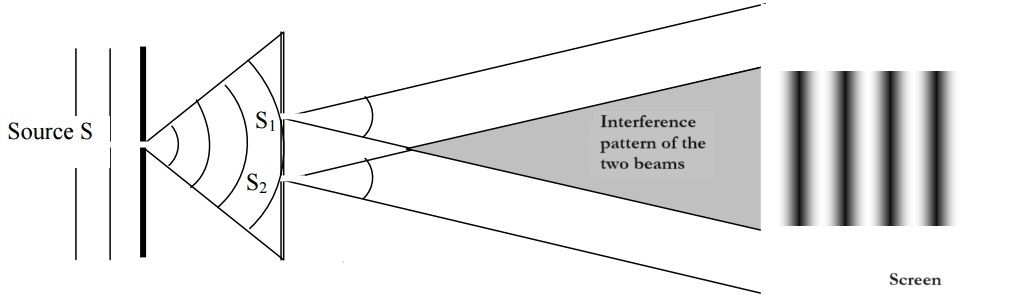
Consider \( S \) as a monochromatic point source illuminating two closely spaced slits \( S_1 \) and \( S_2 \), which are sufficiently far from \( S \). \( S_1 \) and \( S_2 \) act as coherent sources, meaning they are in phase with each other. Both \( S_1 \) and \( S_2 \) diffract light. In the region of space where the two beams overlap, one can observe a series of bright and dark fringes.
The intensity distribution on the observation plane is given by:
\( I=I_0 \cdot \frac {sin^2 ~ \left( \frac{\pi e}{\lambda} sin ~ \theta \right) } { \underbrace{\left( \frac{\pi e}{\lambda} sin ~ \theta \right)^2}_{Terme~ de ~diffraction} } \cdot \underbrace{ cos^2 \left( \frac{\pi a sin ~ \theta}{\lambda}\right)
} _{Terme~ d'interférence} \) (3)
The "principal" intensity maxima separated by \( h \) corresponding to diffraction satisfy the same condition as the minima for a single slit or two slits: \( h = \frac{2 \lambda D}{e} \)
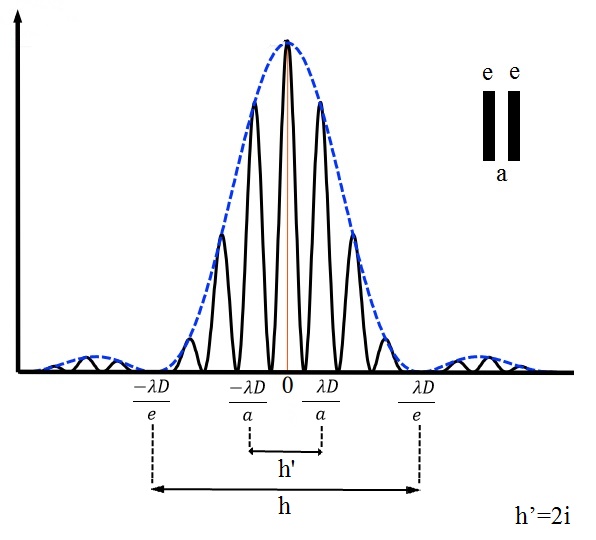
\( \frac{\pi a} {\lambda} sin~ \theta =\pm m \pi~~~~~m=0,1,2... \) order of the principal maximum \( \theta \) very small
\( \Rightarrow sin~ \theta \approx \theta \approx tg~ \theta \approx \frac{h'}{2D}\) hence \(\frac{\pi a}{\lambda} sin~ \theta = \frac{\pi a}{\lambda} \left( \frac{h'}{2D}\right) = \frac{\pi a i}{\lambda D}=\pm m \pi . \)
The distance \( i \) between two consecutive bright fringes is:
\( i=\frac{\lambda D}{a} \) (4)
Diffraction by N identical slits: the grating
It's a system of \( N \) equidistant and identical parallel slits. We observe the same pattern as with two slits but with a different number of interference fringes.
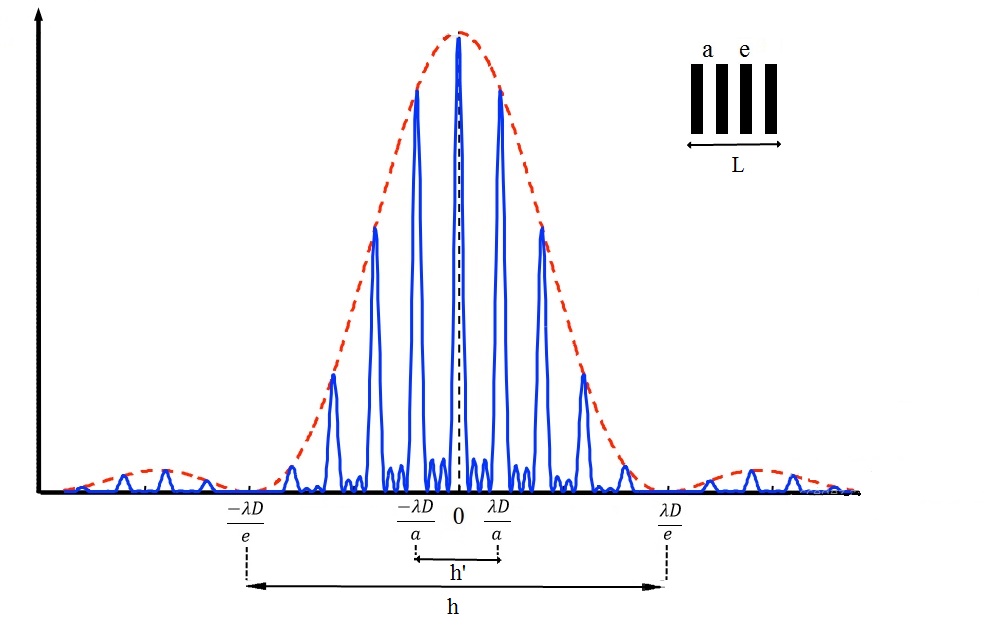
\( I=I_0 \cdot \frac {sin^2 ~ \left( \frac{\pi e}{\lambda} sin ~ \theta \right) } { \underbrace{\left( \frac{\pi e}{\lambda} sin ~ \theta \right)^2}_{ diffraction~term~ (Envelop)} } \cdot \underbrace{ \frac{sin^2 ~ \left( \frac{N \pi a}{\lambda}
sin ~ \theta \right) }{sin^2 ~ \left( \frac{\pi a}{\lambda} sin ~ \theta \right) } } _{interferences ~between ~different ~waves} \) (5)
The main intensity minima separated by \( h \) corresponding to diffraction satisfy the same condition as the minima for a single slit or two slits.
\( h=\frac{2 \lambda D}{e} \) (6)
The fringe spacing is then given as for two slits by:
\( i=\frac{\lambda D}{a} \) (7)
Manipulation
The experimental study will be conducted using a laser emitting monochromatic light with a wavelength \( \lambda = 0.633 \) µm.
The diffraction pattern is observed on a screen located at a distance \( D = 3.20 \) m.
Diffraction by a long narrow slit
To demonstrate the phenomenon of light diffraction, you can set up a simple experiment using a laser and a narrow slit. Here are the steps to carry out this setup:
- Place the laser on a stable surface so that it is aimed towards the slit.
- Position the slit at a certain distance from the laser, ensuring it is aligned properly with the laser beam.
- Position the projection screen at a distance \( D \) from the slit, as mentioned earlier.
- Turn on the laser and observe the diffraction pattern formed on the screen.
Measure \( h \) and deduce the width
of the slit.
Calculate the errors.
The diffraction by two identical parallel slits.
In this part, we are interested in the diffraction of the same monochromatic beam by two slits. In addition to the simple diffraction of the beam, interference phenomena occur.
Perform measurements of \( h \) and \( i \).
Determine \( e \) and \( a \).
Calculate the errors.
Diffraction by N identical slits: the grating.
The objective of this experiment is to generalize the Young's double-slit setup to understand the operation of devices with multiple regularly spaced slits of the same width.
Perform measurements of \( h \) and \( i \).
Deduce \( e \) and \( a \).
Given the width \( L \) of the grating with \( N \) slits, determine \( N = \frac{L}{a} \).
Calculate the errors.
Given: \( L = 36 \) mm.
