المنوال Mode
تعبر قيمة المنوال عن المشاهدة الأكثر تكرارا فهو بمثابة القيمة الشائعة، وقد يكون للبيانات منوال واحد، كما يمكن أن يكون لها أكثر من منوال، كما يمكن أن لا تضم البيانات منوالا.
المنوال لمتغير كمي منفصل
المنوال هو قيمة المتغيرة Xi الأكثر تكرارا في جدول التوزيع التكراري
مثال :
يمثل الجدول التالي عدد أيام التغيب الشهرية عن العمل لمجموعة من عمال مؤسسة ما.
عدد الأيام Xi | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
عدد العمال ni | 22 | 18 | 15 | 25 | 12 | 8 |
الحل:
من الجدول السابق نلاحظ أن أكبر تكرار هو القيمة 25 ومنه فالمنوال هو، وهذا يعني أن الغياب الشائع بين العمال هو 3 أيام شهريا.
المنوال لمتغير كمي متصل
لإيجاد المنوال في حالة متغير كمي متصل، نقوم في البداية بتحديد الفئة المنوالية ثم حساب المنوال. فإذا كانت أطوال الفئات غير متساوية نقوم أولا بتعديل التكرارات حتى تكون الفئات متناسقة بينها، وهنا نميز حالتين:
حالة فئات متساوية الطول
في هذه الحالة الفئة المنوالية هي الفئة التي يقابلها أكبر تكرار ni، ويتم حساب المنوال باستخدام العلاقة التالية:
حيث:
Mo: المنوال
Lo: الحد الأدنى للفئة المنوالية.
ai: طول الفئة المنوالية
delta1: الفرق بين التكرار المطلق للفئة المنوالية والفئة التي تسبقها.
delta2: الفرق بين التكرار المطلق للفئة المنوالية والفئة التي تليها.
مثال :
نأخذ المثال السابق لأجور العمال
الأجر Xi | [10 -20[ | [20 -30[ | [30 -40[ | [40 -50[ | [50 -60[ | [60 -70[ |
|---|---|---|---|---|---|---|
عدد العمال ni | 18 | 30 | 25 | 17 | 12 | 8 |
المطلوب: إيجاد قيمة المنوال
الحل:
بما أن الفئات متساوية في الطول فلا داعي لحساب التكرار المعدل. ونتبع الخطوات التالية
1- تحديد الفئة المنوالية الفئة التي يقابلها أكبر تكرار وهي الفئة 20-30.
2- حساب المنوال بتطبيق العلاقة التالية:
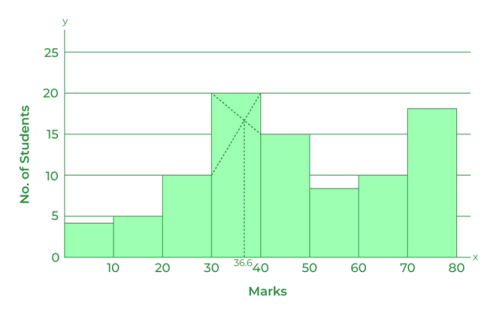
تحديد المنوال بيانيا
يمكن تحديد المنوال بيانيا وذلك من خلال رسم المدرج التكراري للفئة المنوالية والفئتين السابقة واللاحقة لها، حيث نقوم بإيصال بدية المستطيل للفئة المنوالية ببداية المستطيل للفئة اللاحقة لها، ونهاية المستطيل للفئة المنوالية بنهاية المستطيل للفئة السابقة لها. ثم نسقط عموديا نقطة تقاطع المستقيمين على محور الفواصل لنحصل على قيمة المنوال.