Aperçu des sections

  • Méthodes Numériques (C/TD)

    Tout replier Tout déplier


    • forum icon
      Résumé Forum

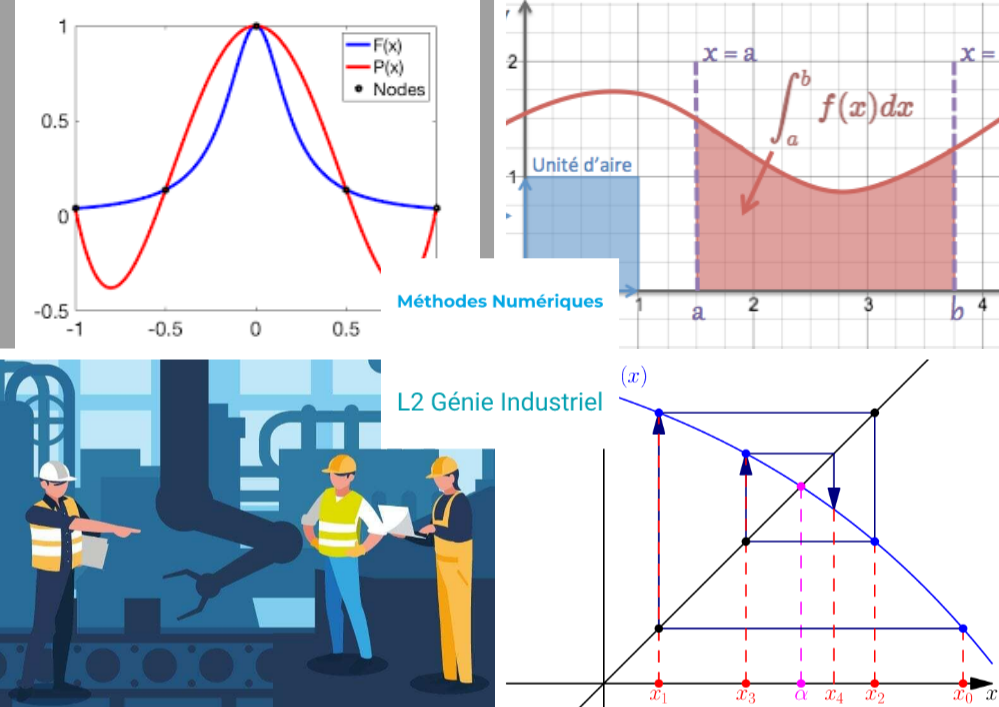
      Les méthodes numériques sont des techniques utilisées pour résoudre des problèmes mathématiques complexes. Elles deviennent nécessaires lorsque la résolution analytique est soit impossible, soit difficile à mettre en œuvre. À l'issue de ce cours, les étudiants seront en mesure d'appliquer ces méthodes pour résoudre divers problèmes mathématiques, tels que les équations non linéaires, l'interpolation, l'intégration, les équations différentielles ordinaires et les systèmes d'équations linéaires. De plus, ils seront capables d'évaluer les erreurs et de comprendre leur impact sur la précision des solutions numériques. 


    • chat icon
      CHAT METHODES NUMERIQUES
    • forum icon
      FORUM METHODES NUMERIQUES

  • Présentation de l'auteur

    Dr. Laribi Imane
    Département de Génie Industriel 
    Faculté de Technologie
    Université de Tlemcen

    imane.laribi@univ-tlemcen.dz

    Disponibilité : Laboratoire MELT 




  • Objectifs de cours

    Pour les étudiants en génie industriel, notamment en deuxième année de licence (L2), la compréhension et la maîtrise des méthodes numériques revêtent une importance capitale. Ces techniques permettent de traiter des problèmes complexes qui sont courants dans le domaine de l'ingénierie industrielle, tels que l'optimisation des systèmes, la modélisation des processus industriels et l'analyse des performances. En acquérant ces compétences, les futurs ingénieurs industriels seront capables de concevoir des solutions précises et efficaces pour des défis pratiques. De plus, la capacité à évaluer les erreurs et à comprendre leur influence sur la précision des résultats est essentielle pour garantir la fiabilité et la robustesse des solutions appliquées dans des contextes industriels.


  • Prérequis

    Pour aborder efficacement le module de méthodes numériques en deuxième année licence Génie Industriel, il est recommandé de disposer des compétences suivantes :

    • Mathématiques Fondamentales : Une solide compréhension des notions d'algèbre linéaire, de calcul différentiel et intégral, ainsi que des équations différentielles. Ces compétences sont essentielles pour aborder les sujets liés à la résolution d'équations non linéaires, l'intégration numérique, et la résolution des systèmes d'équations linéaires.
    •  Algorithmiques : Une compréhension des concepts fondamentaux de l'algorithmique est utile, car les méthodes numériques reposent sur des algorithmes spécifiques pour résoudre divers problèmes mathématiques.
    • Programmation : Des compétences de base en programmation sont nécessaires, car les méthodes numériques sont souvent implémentées à l'aide de langages tels que MATLAB, Python ou C++. Une familiarité avec les principes de programmation vous aidera à coder et tester les algorithmes numériques.
    Assurez-vous de revoir ces compétences avant de commencer le module pour une meilleure compréhension et aussi pour maximiser votre réussite dans le module et tirer le meilleur parti des concepts abordés.



  • Syllabus



  • Chapitre 1 : Résolution des équations non linéaires

    Une équation non linéaire est une équation où la variable inconnue apparaît avec des puissances supérieures à un, ou dans des fonctions trigonométriques, exponentielles ou/et logarithmes, etc. Contrairement aux équations linéaires, les équations non linéaires ne peuvent pas toujours être résolues de manière analytique, c'est pourquoi des méthodes numériques sont souvent utilisées. 

    Ce chapitre présente un aperçu des différentes méthodes de résolution des équations non linéaires. Le chapitre commence par une introduction aux erreurs de calcul, essentielles pour comprendre les limites et la précision des méthodes numériques. Ensuite, il aborde les principales techniques utilisées pour résoudre ces équations, à savoir : la méthode de bissection, la méthode des approximations successives et la méthode de Newton-Raphson. Chacune de ces méthodes sera explorée en détail avec des exemples et des analyses pour illustrer leur fonctionnement et leurs applications en génie industriel.

  • Chapitre 2 : Interpolation polynomiale et approximation

    L'interpolation polynomiale est une technique essentielle dans le domaine des calculs numériques et de l'estimation de valeurs inconnues. En génie industriel, elle est utilisée pour modéliser et prédire le comportement des systèmes à partir de données observées ou expérimentales.

    Ce chapitre approfondira deux des méthodes les plus courantes d'interpolation polynomiale : le polynôme de Lagrange et les polynômes de Newton, qui offrent des approches différentes pour atteindre des résultats similaires.

  • Chapitre 3 : Intégration numérique

    L'intégration numérique consiste à estimer la valeur d'une intégrale définie lorsque celle-ci ne peut pas être calculée analytiquement ou lorsqu'une fonction est connue uniquement par des points discrets. Ce chapitre approfondira deux des méthodes les plus courantes d'intégration numérique : la méthode du trapèze et la méthode de Simpson.

  • Chapitre 4 : Méthode de résolution directe des systèmes d’équations linéaires

    Ce chapitre traite des méthodes directes de résolution des systèmes d'équations linéaires. Dans ces méthodes, la solution du système linéaire est obtenue en un nombre fini d'étapes, dépendant de la taille du système. Ces méthodes sont déterministes, ce qui signifie qu'elles produisent une solution exacte (dans les limites des erreurs d'arrondi) après un certain nombre d'opérations. Dans ce chapitre, l'élimination de Gauss, la décomposition LU et la décomposition de Cholesky seront abordées en détail.


  • Chapitre 5 : Méthode de résolution approximative des systèmes d’équations linéaires

    Les méthodes itératives s'appuient sur des approximations successives pour converger vers la solution. Partant d'une supposition initiale, ces méthodes affinent la solution à chaque itération, améliorant idéalement la précision jusqu'à ce qu'une tolérance souhaitée soit atteinte. Nous explorons dans ce chapitre la méthode de Jacobi et la méthode de Gauss-Seidel.


  • Chapitre 6 : Résolution des équations différentielles ordinaires

     Dans ce chapitre, nous nous concentrerons sur les méthodes de résolution des équations différentielles ordinaires (EDO), et plus particulièrement sur le problème de Cauchy. Le problème de Cauchy, également connu sous le nom de problème de la valeur initiale, consiste à trouver une solution à une équation différentielle compte tenu des conditions initiales en un point spécifique. Ce chapitre traite la méthode d'Euler et de la méthode Runge-Kutta.


  • Ressources Supplémentaires