PRACTICAL WORK OF PHYSICS (MECHANICS)

4. PW2 : STATIC AND DYNAMIC STUDIES OF THE OSCILLATING PENDULUM

1. Goals
  • Highlight the movement of an elementary mechanical system: the oscillating pendulum.
  • Determine the spring stiffness constant by two methods: static and dynamic.
  • Measure the value of an unknown mass from the spring calibration curve.
2. Used Material

  • A support.
  • A metal rod.
  • A spring of negligible mass
  • A box of marked masses.
  • A graduated ruler.
  • A stopwatch.
  • A mass of unknown value.
 PW2_Spring


3. Theory

3.1. Static study
When a mass \( m \) is suspended from a spring, the latter lengthens and exerts a force \( \vec{F} \)  on the object responsible for its elongation; this force is called spring tension.

The elongation of the spring is noted \(x_{eq} \) and is defined by: \(x_{eq} \ = \Delta l_0 = l - l_0\)

where:

    • \( l_0 \) is the empty length of the spring
    • \( l \) is the length of the extended spring.

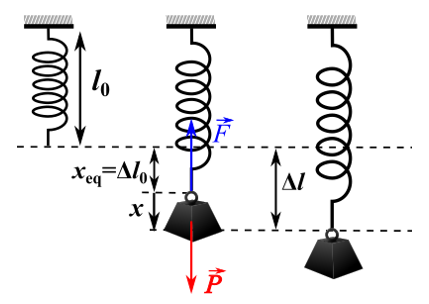
  PW2_Elongation

A stiffness spring \( k \), whose mass will be neglected, is suspended vertically by its upper end from a support.

By applying Newton's first law, we have :

 At Equilibrium  :   \( \vec{P} + \vec{F}=\vec{0} \)  with  \( P = mg \)  and  \( F = k \Delta l_0 =k x_{eq} \)

From where, by projection on the axis of movement oriented vertically, we obtain:

\( P-F=0 \Rightarrow mg-k \Delta l_0 =0  \Rightarrow mg-k x_{eq} =0 \)

Thus, we have :

\( x_{eq}=\Delta l_0 = mg/k \)               (1)

3.2. Dynamic study
Using the previous spring, in addition to its first elongation due to the clinging mass, we stretch the spring with a distance (see the figure above).
By applying Newton's second law, we have :  \( \vec{P} + \vec{F}=m\vec{a} \) where (\( \vec{a} \) is the acceleration vector).
By projection on the axis of movement oriented vertically, we get : \(p_x - F_x=a_x\)
Using the relations : \(F_x = k \Delta l \) with \(\Delta l =\Delta l_0 +x = x_{eq} +x \) and \( a_x =\ddot{a} \), we get:

\(mg-k(\Delta l_0 + x ) = m \ddot{x} \)

\(mg-k(\Delta x_{eq} + x ) = m \ddot{x} \)

Using the relation (1), we obtain the differential equation of the oscillatory movement: \( \ddot{x} +\frac{k}{m}x=0 \)

with : \( \omega^2=\frac{k}{m} \) and \( \omega =\frac{2\pi}{T} \) 

    • \(\omega\) : The pulsation
    • \(T\) : The period

We can thus determine the expression of the period of the pendulum:

\( T=2\pi \sqrt{\frac{m}{k}} \)        (2)

Physically, the period \(T\) represents the time of one oscillation.

4. Experimental Procedure

4.1. Static Study
  1. Start by hanging the spring from the horizontal rod.
  2. Attach the ruler so you can take precise measurements.
  3. Measure the empty length \(l_0\) of the spring.
  4. Then you must first suspend the weight rack to be able to place the masses on it.
  5. Different known masses (\(m\)) of increasing values (see the table on the PW-sheet) are attached to the spring:
    • At equilibrium, measure the corresponding elongations (\(X=x_{eq}\)), taking into account the mass of the weight rack.
    • For each mass, take a minimum of three measurements (each student will take one measurement).
    • Record your results in the table.
  6. To preserve the spring, you must unhook the mass directly after performing the measurement. Never leave masses attached to the spring!!.
  7. On a millimeter sheet, draw the calibration curve of the spring \(x_{eq}=f(m) \).
4.2.Determination of the Unknown Mass of a body

We want to determine the unknown mass \(m\) of a body from the calibration curve of the spring, for this :

  1. Take the device used previously and put the unknown mass to the spring.
  2. Measure the elongation \(x_{eq} \) of the spring.
  3. Use the spring calibration curve to determine the value of the mass\(m \).
4.3.Dynamic Study

  1. Resume the previous device. Attach a known mass \(m\) to the spring.
  2. Stretch the spring (taking it away from its equilibrium position) a small distance \(x\), perfectly vertically, then let go of the mass without initial velocity.
  3. Let the mass oscillate and measure the period of the oscillations \(T\) (read and carefully follow the measurement instructions on the sheet hung in the laboratory).
  4. For each mass, take a minimum of three measurements (Each student will take one measurement).
  5. Fill in the measurement table on the PW-sheet.
  6. On a millimeter sheet, draw the calibration curve of the spring \(T^2=f(m) \)


Tags: