La focométrie
But
Le but du TP est de déterminer la distance focale de divers lentilles minces par les méthodes suivantes :
- Objet à l'infini,
- d'auto collimation,
- points conjuguées,
- Bessel,
- Silberman,
- Badal.
Définition
Une lentille est un milieu transparent délimité par deux dioptres, qui peuvent tous deux être sphériques ou l'un être sphérique et l'autre plan (on les nomme souvent lentilles sphériques).La droite qui joint les centres des deux dioptres sphériques s'appelle
l'axe principal ou axe optique.
Les rayons de courbure de la lentille sont les rayons de courbure \(\left|R_1 \right|\) et \(\left|R_2\right|\)des deux dioptres sphériques. Lorsque l'une des faces est plane, son rayon de courbure est pris par
convention égal à \( \infty \).
Une lentille mince est une lentille où son rayon est très grand devant son épaisseur.
On distingue deux types de lentilles : la lentille à bords minces, qui est convergente, et la lentille à bords épais, qui est divergente.Il existe six formes possibles
de lentilles :
- lentilles biconvexes,
- lentilles biconcaves,
- lentilles plan-convexe,
- lentilles plan-concaves,
- ménisques à bords minces,
- ménisques à bords épais.
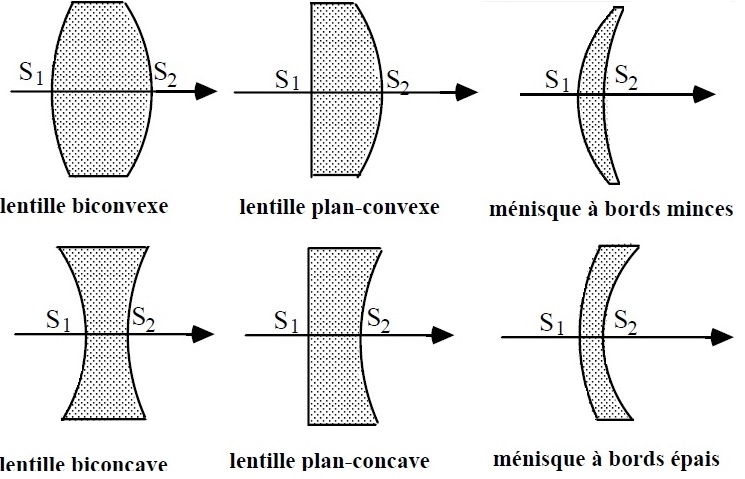
Figure 1: Différents types de lentilles et leur symbole
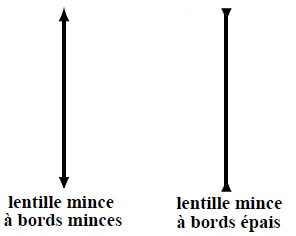
Figure 2: Différents types de lentilles et leur symbole
Foyers objet et image, distance focale
Foyer image
Le foyer image \( f_0 \) est le point de l’axe optique dont l’objet est à l’axe. Tout rayon incident parallèle à l’axe optique d’une lentille émerge en passant par \( f_0 \) \( \frac{1}{f'} =(n-1) \frac{1}{R_1} - \frac{1}{R_2} \)Son abscisse \( f_0 = P_0(F_0) \) s’appelle la distance focale image. La formule des lentilles nous donne :\( \frac{1}{f'}= (n-1) \frac{1}{R_1}- \frac{1}{R_2} ~~~~~~~~~(1)\)
Foyer objet
Le foyer objet, noté \( f \), est le point de l’axe optique tel que l’image formée soit située à l’infini sur cet axe. Tout rayon incident passant par \( F \) ressort du système optique de manière parallèle à l’axe optique. Sa distance par rapport au centre optique, notée \( f =P(F)\), est appelée distance focale objet. La formule associée est la suivante :
\( - \frac{1}{f}= (n-1) \frac{1}{R_1}-\frac{1}{R_2} ~~~~~~~~~(2) \)
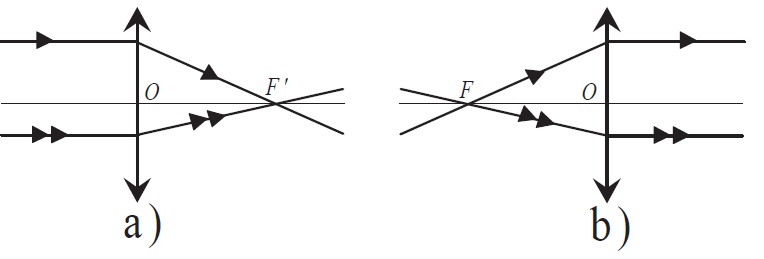
Figure 3: a) Foyer image d’une lentille convergente. b) Foyer objet d’une lentille
convergente.
Formation des images
Pour construire l'image d'un tel objet AB plan et perpendiculaire à l'axe, il suffit de construire l'image B' du point B situé hors de l'axe. Comme la lentille est aplanétique (conditions de Gauss), le point A' est
obtenu par projection orthogonale de B' sur l'axe optique.
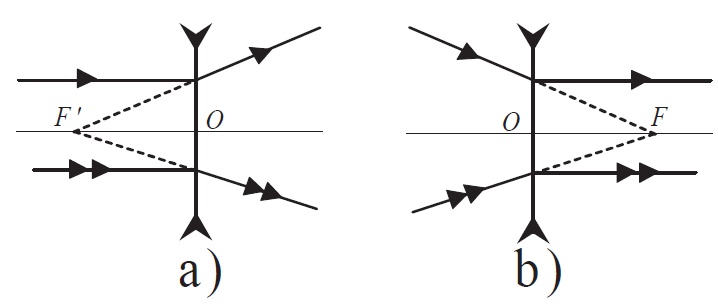
Figure 4: a) Foyer image d’une lentille divergente. b) Foyer objet d’une lentille
divergente.
- Avant toute chose, il faut placer l'objet. Si l'objet AB est réel, il se trouve forcément à gauche de la lentille et les rayons émergent de chaque point de l'objet. Si l'objet est virtuel, il se situe à droite de la lentille et les rayons "objets" se dirigent vers l'objet mais sont réfractés avant d'atteindre celui-ci.
- Pour trouver l'image d'un point, il faut choisir des rayons dont on connaît le comportement.
- Un rayon horizontal arrivant sur une lentille convergera en F' si elle est convergente et divergera en semblant provenir de F' si la lentille est divergente.
- Un rayon passant ou se prolongeant en F ressortira horizontalement.
- Un rayon passant par O ne sera pas dévié.
- Une fois les rayons tracés, on détermine si l'image est réelle ou virtuelle. Si les rayons issus de B se coupent effectivement en B', alors B' est une image réelle que l'on peut capturer sur un écran. Si les rayons issus de B divergent après réfraction en semblant provenir de B' , alors B' est une image virtuelle visible à l'œil nu mais que l'on ne peut pas capturer directement sur un écran.
Relation des lentilles minces
Relation de conjugaison
Relation de conjugaison de Newton
Considérons, sur la figure 5 , les triangles rectangles semblables ABF et OJF,
A'B'F' et OIF'. Nous voyons que :
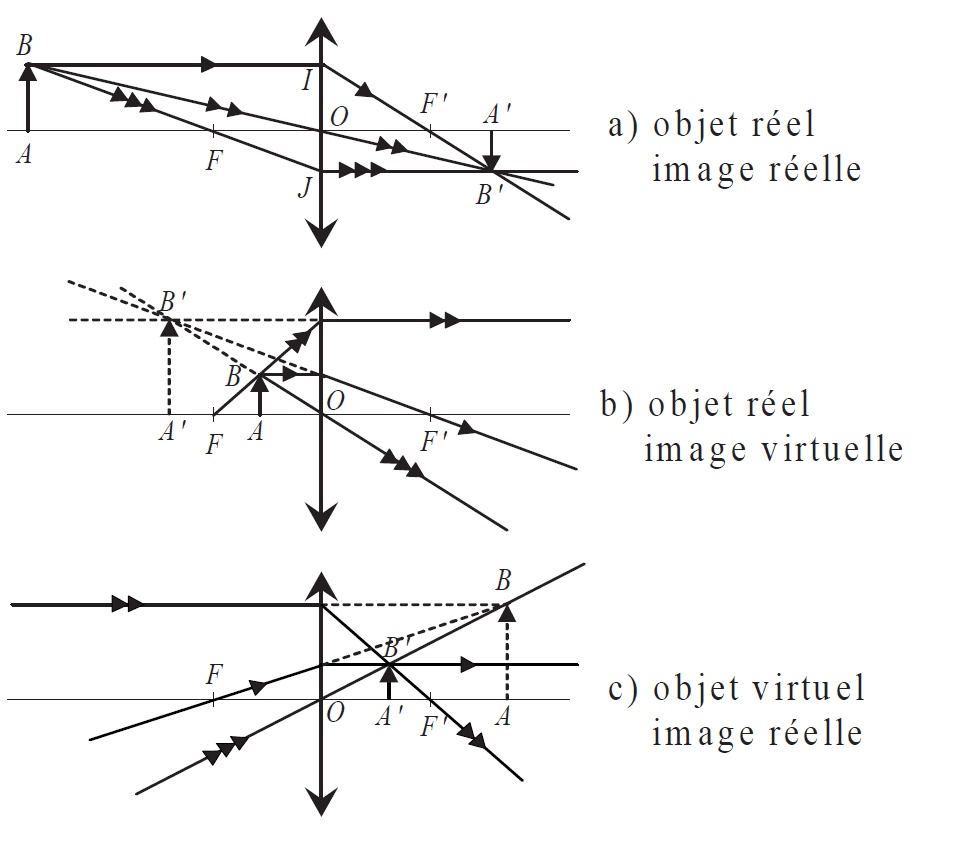
Figure 5: Construction d’images pour une lentille convergente.
\( \frac{\overline {AB}}{\overline {OJ}}=\frac{\overline {FA}}{\overline {FO}}=\frac{\overline {FA}}{\overline {f}} ~~~~~~~~~(3)\)
\( \frac{\overline {A'B'}}{\overline {OI}}=\frac{\overline {F'A'}}{\overline {F'O}}=\frac{\overline {F'A'}}{f'} ~~~~~~~~~(4)\)
Or \( \overline {OJ}=\overline {A'B'} \) et \( \overline {OI}=\overline {AB} \)
d'où:
\( \frac{\overline {F'A'}}{f'}=\frac{f}{\overline {FA}} ~~~~~~~~~(5)\)
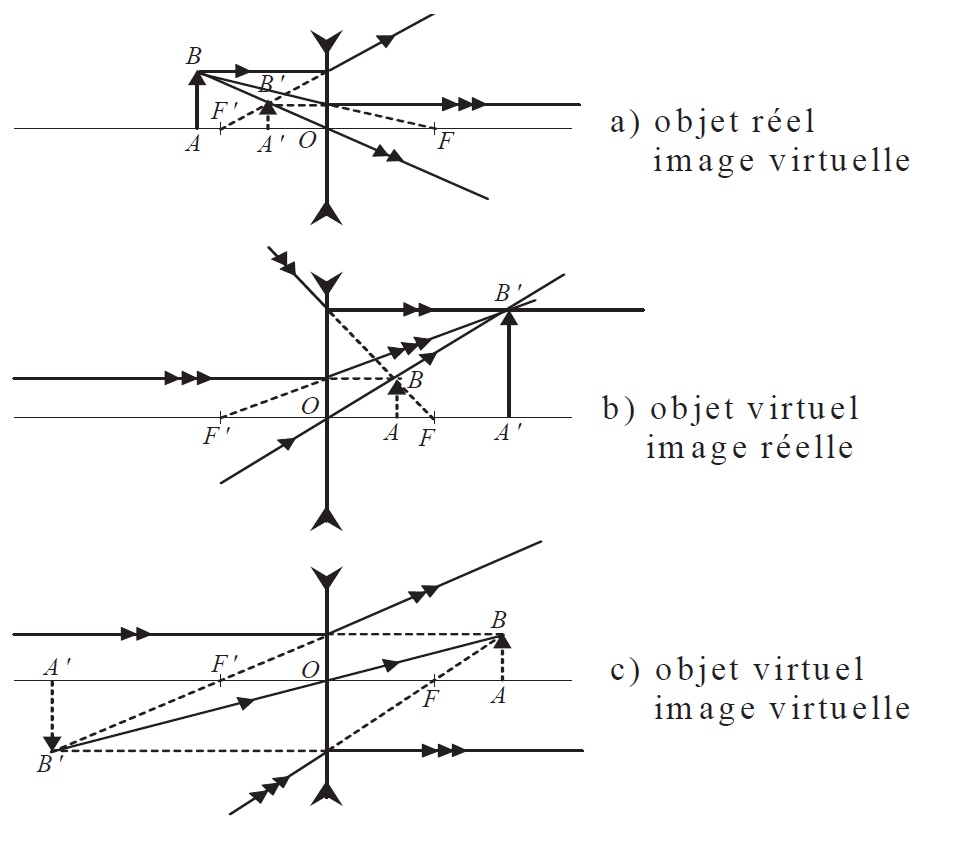
Figure 6: Construction d’images pour une lentille divergente.
De cette dernière égalité, on tire la relation de conjugaison de Newton encore
appelée relation de conjugaison avec origine aux foyers :
\( \overline{FA} . \overline{F'A'}= f .f'=-f'^2 ~~~~~~~~~(6) \)
Relation de conjugaison de Descartes
Partons des relations suivantes : \( \overline{FA} = \overline{FO} +\overline{OA} = f' +\overline{OA} \) et \( \overline{F'A'} = \overline{F'O} +\overline{OA'} = -f' +\overline{OA'} \). En les reportant dans la relation de conjugaison de Newton, nous obtenons :
\( (f' + \overline{OA}).(-f' + \overline{OA'}) = -f'^2 \Longleftrightarrow \overline{OA} .\overline{OA'} + f' .\overline{OA'} -f' . \overline{OA}=0 \). Soit, en divisant par \( \overline{OA}.\overline{OA'}.f' \),
\( \frac{1}{f}=\frac{1}{\overline{OA}}-\frac{1}{\overline{OA'}}=0 ~~~~~~~~~(7)\)
Cette dernière égalité constitue la relation de conjugaison de Descartes encore appelée relation de conjugaison avec origine au centre :
\( \frac{1}{f'}=\frac{1}{\overline{OA'}}-\frac{1}{\overline{OA}} ~~~~~~~~~(8)\)
Grandissement
Rappelons que le grandissement transversal est le rapport algébrique de la taille de l’image à celle de l’objet :
\( \gamma = \frac{\overline{A'B'}}{\overline{AB}} ~~~~~~~~~(9) \)
Si \( \gamma >0 \) , l’image est dite droite, sinon elle est dite renversée.
Grandissement avec origine aux foyers
Les relations 3 et 4 impliquent que :
\( \gamma = \frac{\overline{A'B'}}{\overline{AB}}= \frac{\overline{F'A'}}{f'}= - \frac {f}{\overline{FA}} ~~~~~~~~~(10) \)
Grandissement avec origine au centre
La relation de grandissement se démontre aisément en considérant dans la figure 5 a le rayon liant \( B \) et \( B' \)et passant par le centre optique \( O \). Ce rayon n’étant pas dévié, on obtient immédiatement que :
\( \gamma = \frac{\overline{A'B'}}{\overline{AB}}= \frac{\overline{OA'}}{\overline{OA}} ~~~~~~~~~(11)\)
Remarque : Toutes les formules que nous venons d’établir sont valables aussi bien pour les lentilles convergentes que pour les lentilles divergentes, ceci quelle que soit la nature de l’objet ou de l’image.
Manipulation
Vous disposez d’un banc d’optique gradué, tous les éléments (lentilles, objet, écran ...) se montent sur des pieds munis de repères permettant la mesure sur celui-ci.
Méthode de l'objet à l'infini
On sait que l’image d’un objet à l’infini se situe dans le plan focal image de la lentille convergente. En se plaçant sur le banc d’optique, on va utiliser cette propriété pour mesurer la distance focale de la lentille convergente.
Manipulation
Placer l’objet à une extrémité du banc optique, et l’écran à l’autre extrémité du banc, de telle sorte que la distance entre l’objet et l’écran soit très grande devant la distance focale ( son ordre de grandeur doit être connu).
Insérer la lentille convergente entre l’objet et l’écran, et trouver la position pour laquelle on obtient une image nette sur l’écran. En considérant l’objet comme étant à l’infini, la distance entre la lentille et l’écran est alors égale à la distance focale.
Mesurer f et évaluer l’incertitude \( \Delta f \) critiquer les résultats obtenue.
Méthode d'auto-collimation
On place contre la face de sortie de la lentille un miroir plan, on déplace l’ensemble (lentille + miroir) jusqu’au moment où l’image \( A'B' \) de \( AB\) apparaît nette, sur la diapositive objet mais avec une inversion \( (\overline{A'B'}=-\overline{AB}) \). L’objet est alors au foyer objet de la lentille : \( \overline{AO}= \overline{FO}=f' \)
L’objet étant situé dans le plan focal objet, l’image en sortie de lentille est à l’infini. Le miroir inverse géométriquement ce faisceau, et ainsi, pour le trajet retour, le faisceau incident provient de l’infini. En retraversant la lentille, les rayons convergent dans le plan focal, et donc sur ’objet. Le miroir doit être légèrement incliné par rapport à l’axe optique pour que l’image ne se superpose pas complètement à l’objet.
Manipulation
Placer la lentille convergente devant l’objet étendu \( AB \) et disposer juste derrière la lentille un miroir plan.
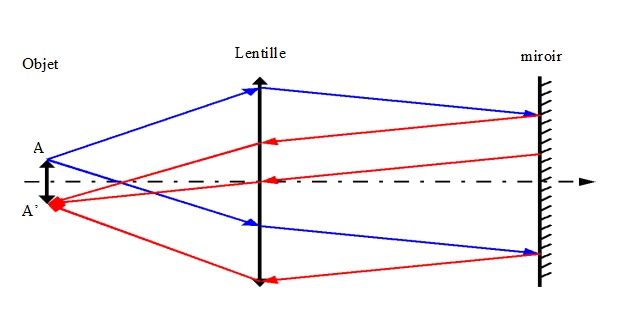
Figure 7: Méthode de mesure par auto collimation.
Déplacer l’ensemble Lentille, Miroir jusqu’à ce que l’image de l’objet apparaisse nette, de même taille et renversée dans le plan de l’objet \( (\gamma =-1) \).
La distance entre l’objet et la lentille est alors égale à la distance focale : \( f'=\overline{AO} \).
Calculer f et évaluer l’incertitude \( \triangle f \) critiquer les résultats obtenue.
Méthode des point conjuguées
Dans cette méthode, le mode opératoire consiste à repérer les positions \( OA = p \) et \( OA' = p' \) de l’image \( (A'B') \) d’un objet \( (AB) \) donnée par la lentille \( (L) \). A l’aide de la relation de conjugaison d’une lentille, on peut déterminer la distance focale \( f \).
Méthode de Bessel
Soit un objet AB situé à une distance \( (D) \) d’un écran \( (E) \) où on visualise l’image \( A'B' \) donnée par une lentille convergente \( (L1) \) de distance focale (f). Il est possible de trouver deux positions \( O_1 \) et \( O_2 \) qui donnent l’image \( A'B' \) sur l’écran \( (E) \) avec la condition \( D > 4f \). La distance focale f de la lentille est donné par:
\( f'=\frac{D^2-d^2}{4D} ~~~~~~~~~(12)\)
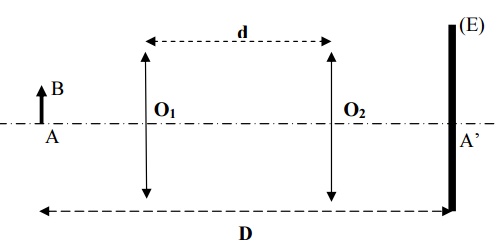
Figure 8: Méthode de mesure par la méthode de Bessel.
Démonstration- On pose \( \overline{O_1A} = p \) et \( \overline{AA'}= D \)
On en déduit: \( \overline{O_1A'} = \overline{O_1A}+\overline{AA'}\)
Soit: \( \overline{O_1A'} = p + D\)
On applique maintenant la formule de Descartes:
\( \frac{1}{p + D}-\frac{1}{p}=\frac{1}{f'_1}\)
\( p(p + D) = f'_1 (p - p - D)\)
\( p^2 + Dp + Df'_1=0\)
On résout cette équation du 2nd degré en \( p\). Pour cela, on écrit le discriminant: \( \Delta= D^2-4Df'_1=D(D-4f'_1)\)
Il y a deux positions \( p_1\) et \( p_2\) si ( \\Delta>0\), soit: ( \D>4f'_1\)
Finalement: \( D_{min}=4f'_1\).
Dans ces conditions, les deux positions sont:
\( p_1= \frac{-D+\sqrt{D^2-4f'_1}}{2}\)et \(p_2= \frac{-D-\sqrt{D^2-4f'_1}}{2}\)On a: \(\Delta< D^2\) soit \(\sqrt{\Delta}< D\).
On en déduit que \(p_1 < 0\) et \(p_2 < 0\): les deux positions calculées correspondent bien à un objet réel.
De plus, on a bien: \(\mid p_2\mid >\mid p_1\mid\).
2. On a: \(d = p_1 - p_2\), \(d = \sqrt{\Delta}\), \(d^2=\Delta\) et \(d^2 = D^2- 4Df'_1\)
Finalement, on trouve la formule de Bessel:
\( f'=\frac{D^2-d^2}{4D} \)
ManipulationEn fixant la distance \( (D) \) entre l’objet et l’écran (prendre la valeur maximale sur le banc optique) déterminer les deux positions \( O_1 \) et \( O_2 \) de la lentille L1 qui donnent une image nette sur l’écran \( (E) \).
Noter les valeurs de \( D \) et \( d \). Évaluer l’incertitude sur ces valeurs, \( \Delta D \) et \( \Delta d \).
En déduire la distance focale de\( L_1 \) f et évaluer l’incertitude \( 4f \)critiquer les résultats obtenue.
Méthode de Silberman
C’est un cas particulier de la méthode de Bessel est celui où \( D=4.f \) . Il n’existe alors qu’une seule position de la lentille qui conjugue l’écran et l’objet, avec un grandissement \( \gamma=-1 \).
ManipulationOn opère par tâtonnement, on commence comme pour la méthode de Bessel à former les 2 images nettes pour \( D = 50cm \). Puis on diminue \( D \) de cm en cm tout en formant les images nette distantes de d avec la lentille, on observe que d diminue jusqu’à avoir \( d=0\) (superposition des 2 images). Retrouver\( f \) et \( 4f \).
Méthode de Badal
La méthode de Badal est une méthode de focométrie de détermination de distance focale de lentille divergente. En effet les méthodes vues précédemment ne sont applicable qu’aux lentilles convergentes.
Afin de déterminer la distance focale d’une lentille divergente, on doit utiliser au préalable deux lentilles convergentes de focale connue.
On considère une lentille mince divergente de focale \( f'_3 \) inconnue, de centre \( O \), de foyers image \( F' \) et objet \( F \).
Pour déterminer cette focale f0, on va faire deux montages successifs. Premier montage : sans la lentille divergente
On utilise deux lentilles convergentes \( L1 \) et \( L2 \)de foyers objets respectifs \( F1 \) et \( F2 \), et de foyers images respectifs \( F'1 \) et \( F'2 \) .
On met un objet \( A\) sur l’axe optique au foyer objet \( F2 \) de la lentille \( L2 \). Son image se trouve en \( A'= F1' \), le foyer image de \( L1 \) :
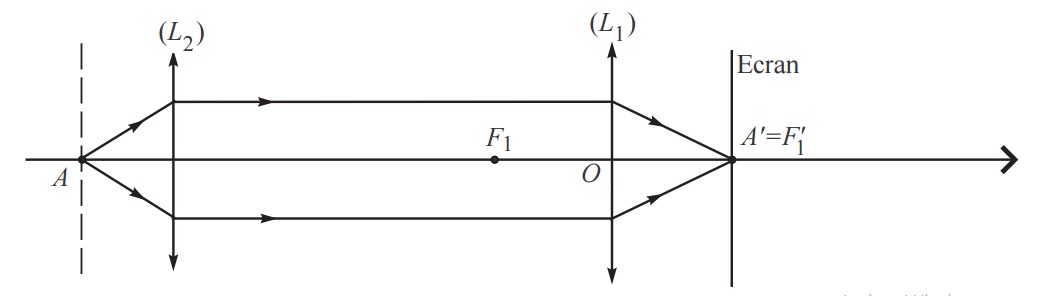
Figure 9: Premier montage : sans la lentille divergente de la méthode de Bessel.
\( A=F_2\rightarrow \infty \rightarrow A'= F'_1 \)
Second montage : avec la lentille divergente On intercale entre les deux lentilles convergentes la lentille divergente \( L_3 \) de focale inconnue au foyer objet \( F1 \) de \( L1 \).
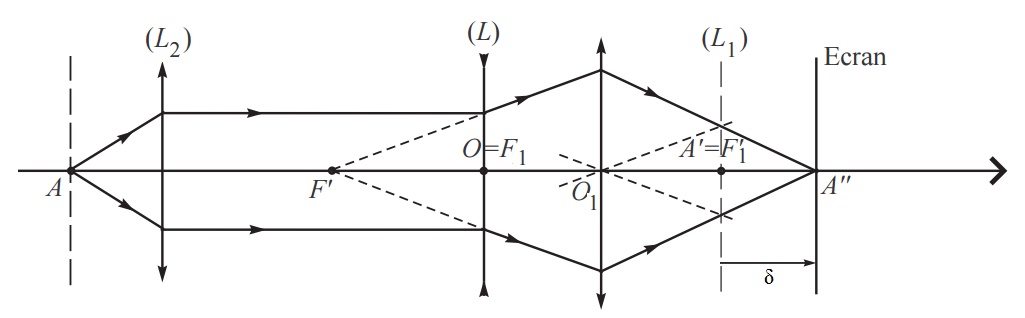
Figure 10: Second montage : avec la lentille divergente de la méthode de Bessel.
La nouvelle image de \( A \) se trouve en \( A'' \) :
\( A=F_1 \rightarrow \infty \rightarrow F'\rightarrow A'' \)
\( F'_0 \) est le foyer image de \( L_3 \), \( A' \) est son image à travers \( (L1)\).
La formule de Newton appliquée à \( (L1)\) pour les points conjugués \( (F'_3,A') \) donne :
\( \overline{F'A'} .\overline{FF'_3}=-f'^2 \)
avec ici \( \overline{F'A'}=\delta \) et \( \overline{FF'_3}=\overline{OF'_3}=f'_3 \)
on obtient : \( \delta f'_3=f'^2 \) d’où :
\( f'_3=\frac{f_1^2}{\delta} ~~~~~~~~(13) \)
ManipulationPlacer la lentille \( L_2 \) convergente à la distance \( f_2=20~cm \) de l’objet. \( L_2 \) donne alors une image à l’infinie (on ne peut pas l’obtenir sur l’écran). Placer la lentille \( L_1 \) à la suite de \( L_2 \) à une distance \( L_2L_1=30 ~cm >f_1\) . L’image de l’objet est alors au foyer \(F'_1\) image de \( L_1 \). On placera l’écran sur ce foyer \(F'_1\) . Noter cette position de l’écran.
Placer la lentille divergente \(F_3\) de distance focale inconnue et à déterminer dans le plan focal objet de \( L_1 \) (distance \( L_3 - L_2 \) = distance \( L_1 \) - Ecran). L’image est par conséquent éloignée (n’est plus sur l’écran). Retrouver l’image nette en déplaçant l’écran d’une distance \( \delta \). Déterminer \( \delta \) et \( \Delta \delta \). La distance focale \( f_3 \) de \( L_3 \) est alors obtenue par la formule de Newton : \( f'_3=f_1^2 / \delta \)
