TP Physique1

• A carriage whose mass m is labeled above.
• An inclined plane of length  L = 100 cm.
• A friction block.
• Two optical forks.
• A graduated ruler.
• A digital stopwatch

III. THEORY :

III.1. Movement without friction :

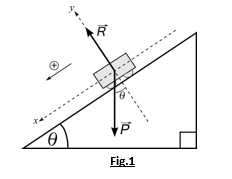
A carriage of mass m slides on an inclined plane that makes an angle  with the horizontal plane (see Fig.1).

The projection on the axis of movement x, gives us :

The equation of motion of the carriage can be written in the form :

Hence, the expression of the distance d traveled by this trolley, for an

initial speed of zero (v₀ = 0)  is :

III.2. Movement with friction :

The carriage is now replaced by a friction block. This block is released, without initial speed, from the top of the inclined plane (see Fig.2). The application of FPD principle gives us:

f  being the frictional force which is added in this case and a^' is the acceleration vector.

Projecting equation (3) onto the x axis, we get:

µ_d  is the dynamic coefficient of friction.

 The projection of equation (3) on the  axis, gives us :

The equation of motion of the carriage can be written in the form:

Hence the expression of the distance  traveled by this block, for an initial speed of zero ( v₀ =0) is :

IV. EXPERIMENTAL PROCEDURE

IV.1. Movement without friction :

 In this part, we vary the distance between the two optical forks and we measure the time necessary for the carriage to travel this distance, taking an initial speed of zero.

1. Set the angle of inclination of the plane to 5°.

2. Place the carriage on the plane, so that its cursor is at the limit of the beam of the optical fork. This is the device that starts the stopwatch. If this instruction is not respected, the results will be falsified by the non-zero initial speed of the carriage when the stopwatch is started.

3. For different distances d of increasing values between the two optical forks (see the table in the TP-sheet), measure the corresponding times t. For each distance, take a minimum of three measurements (each student will take one measurement). When the carriage cursor crosses the beam of the second optical fork, the stopwatch stops and it displays the time elapsed for crossing this distance. Record your results in the measurement table.

4. On a millimeter sheet, draw the requested curve.

IV.2. Movement with friction :

IV.2.1. Determination of the dynamic coefficient of friction :

1. Consider the previously used device.

2. Set the angle of inclination of the plane to 20°.

3. Replace the carriage with the friction block.

4. Put the block on the side that contains a single face of felt.

5. The block must be placed on the plane, so that its cursor is at the limit of the beam of the optical fork.

6. Drop the block with no initial velocity. Measure the duration (time) of the movement for the different distances between the two optical forks (see the table in the TP-sheet). Record your results in the measurement table.

7. On a millimeter sheet, draw the required curve.

IV.2.2. Determination of the coefficient of static friction :

1. Take the previously used device.

2. Set the angle of inclination of the plane to 0°.

3. Increase the angle of the incline until the block slides. Note the value of the angle.

4. Calculate the coefficient of static friction.

V. THEORETICAL QUESTIONS (IMPORTANT) :

1. Determine the expression of the acceleration for the movement without friction (case III.1.) of the carriage  depending on the earth's acceleration g  .

2. Determine the expression of the acceleration for the movement with friction (case III.2.) of the carriage  depending on the earth's acceleration  and the coefficient of dynamic friction  µ_d .

2. Determine the expression for the coefficient of static friction µ_s  depending on the angle of the inclined plane   .