Définition
Le périodogramme est un estimateur de la DSP[1] basé sur la Transformée de Fourier Discrète (TFD[2]) qui est donnée par l'équation (1). La DSP estimée est le module de la TFD du signal à analyser.
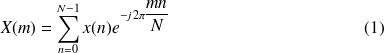
La TFD peut être calculée par la fft[3] qui est un algorithme rapide d'une structure dyadique. La Transformée de Fourier Rapide (TFR) d'un signal x (n) peut être calculée par la fonction MATLAB selon la syntaxe suivante :
Avec x est le signal à analyser, N est le nombre d'échantillons sur lequel est calculée la fft et X est le vecteur complexe contenant les coefficients sinusoïdaux.
Le paramètre n est optionnel et est utilisé pour modifier la longueur des données à analyser: si n<length(x), alors l'analyse est effectuée sur les n premiers échantillons; ou bien, si n>length(x), alors x est complété par des zéros afin qu'il soit d'une longueur égale à n.
Le temps de calcul dépends de la longueur du signal et est meilleur si ce nombre d'échantillons est puissance de 2. Par exemple, sur une même machine, la FFT d'un signal de 4096 échantillons dure environ 2, 1 secondes, mais ça nécessite 7 secondes si le signal est de 4095 échantillons, et 58 secondes si la séquence est de 4097 points. Il est alors judicieux que la longueur de la séquence à traiter par un algorithme FFT soit une puissance de 2. Il est à noter que ces temps de calcul sont effectué sur une même machine afin d'assurer la cohérence de la comparaison. Ce temps de calcul change évidemment selon la machine utilisée pour effectuer le calcul.
La magnitude du spectre de puissance est obtenue en appliquant la fonction abs
qui permet de calculer le module du vecteur complexe X :
La phase du spectre de puissance est calculée par la fonction angle :
La fonction angle permet de calculer l'arc–tangente de la partie imaginaire divisée par la partie réelle du vecteur X.






