Formule de Taylor
Définition :
1/ Formule de Taylor pour les polynomes :
Soit
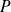un polynome de degré
et un point
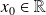, alors :
.
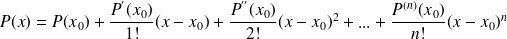Définition :
2/Formule de Taylor pour les fonctions :
L'idée est de trouver une approximation d'une fonction non polynomiale par un polynôme au voisinage d'un point.
Complément :
2.1/Théorème de Taylor-Lagrange :
Soit
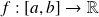une fonction de classe
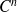dans
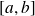et admettant une dérivée d'ordre
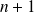dans
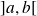, alors
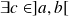telle que :
.
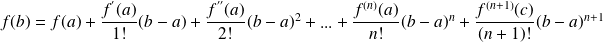Avec :
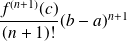c'est le reste de Lagrange.
2.2/ Formule de Taylor-Young :
Soit
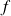une fonction de classe
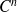dans un intervalle
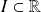contenant
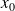, alors,
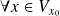il existe une fonction
(reste le Young) définie dans un voisinage de
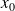telle que :
,
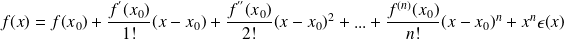avec
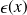tend vers 0 quand
tend vers
.
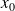Remarque :
La formule de Taylor-Lagrange peut être écrite au voisinage d'un point
.
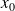La formule de Maclaurin-Lagrange= formule de Taylor-Lagrange en
.
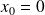Exemple :
Trouver le développement de Taylor-Lagrange d'ordre
de
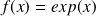en 0 (i.e formule de Maclaurin-Lagrange).
On a
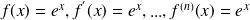, alors le développement de Taylor-Lagrange d'ordre
est :
.
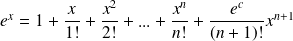