Développement limité
Définition :
Soit
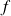 une fonction définie dans un intervalle
une fonction définie dans un intervalle
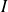 contenant
contenant
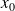 .
.
On dit que
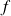 admet un développement limité d'ordre
admet un développement limité d'ordre
 en
en
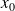 si :
si :
 et
et
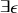 une fonction définie au voisinage de
une fonction définie au voisinage de
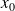 telle que :
telle que :
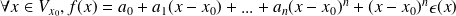 ,
,
avec
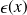 tend vers 0 quand
tend vers 0 quand
 tend vers 0.
tend vers 0.
Remarque :
Si
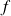 est de classe
est de classe
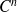 au voisinage de
au voisinage de
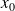 , on peut choisir :
, on peut choisir :
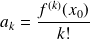 (d'après la formule de Taylor).
(d'après la formule de Taylor).
Exemple :
Le
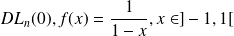 est :
est :
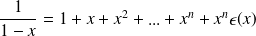 , avec :
, avec :
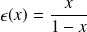 .
.
Définition :
Opérations sur les D.L :
1/Somme : si
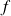 et
et
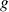 admettent des
admettent des
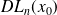 , alors
, alors
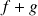 admet
admet
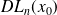 dont la partie régulière est la somme des parties régulières.
dont la partie régulière est la somme des parties régulières.
2/Produit : si
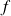 et
et
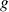 admettent des
admettent des
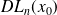 , alors
, alors
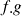 admet
admet
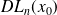 dont la partie régulière est le produit des parties régulières (on ne conservant que les termes de puissances inférieures ou égale à
dont la partie régulière est le produit des parties régulières (on ne conservant que les termes de puissances inférieures ou égale à
 ).
).
3/Quotient : si
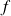 et
et
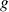 admettent des
admettent des
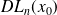 et si
et si
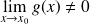 , alors
, alors
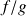 admet
admet
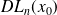 dont la partie régulière est obtenue par division euclidienne selon les puissances croissantes jusqu’à la puissance
dont la partie régulière est obtenue par division euclidienne selon les puissances croissantes jusqu’à la puissance
 .
.
Remarque :
Si on a le D.L d'une fonction au voisinage de
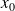 , on peut se ramener au D.L au voisinage de 0, en posant :
, on peut se ramener au D.L au voisinage de 0, en posant :
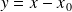 .
.






