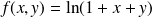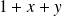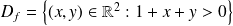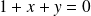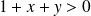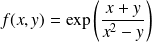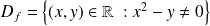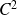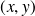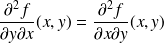Fonction de deux variables
Domaine de définition
On considère une fonction
 défini par :
défini par :
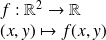
L'ensemble de définition (domaine de définition) de
 , noté
, noté
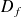 , est le sous-ensemble de
, est le sous-ensemble de
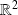 formé des couples de réels tels que
formé des couples de réels tels que
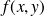 existe.
existe.
Exemple :
Soit
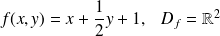 .
.Soit
 est le plan
est le plan
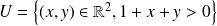 , C'est au-dessus de la droite d'équation
, C'est au-dessus de la droite d'équation
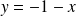 .
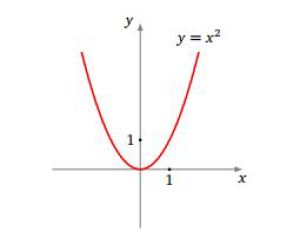
.Soit
 est tous les points du plan qui ne sont pas sur la parabole d'équation
est tous les points du plan qui ne sont pas sur la parabole d'équation
 .
.
Représentation graphique
On considère l'espace euclidien[1] rapporté à un repère orthonormal
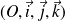 . La représentation graphique d'une fonction
. La représentation graphique d'une fonction
 de
de
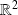 vers
vers
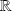 est l'ensemble des points de cet espace de coordonnées
est l'ensemble des points de cet espace de coordonnées
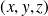 tels que :
tels que :
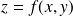 .
.
Cette représentation graphique est une surface dans l'espace.
Exemple :
Soit
 .
.
la surface représentative de la fonction
 est un plan de l'espace, d'équation
est un plan de l'espace, d'équation
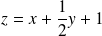 . Cette fonction est dite affine.
. Cette fonction est dite affine.
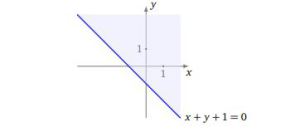
Il faut que
Pour tracer cet ensemble, on trace d'abord la droite d'équation
|
Limites
Toutes les propriétés des limites des fonctions à une variable s'étendent aux fonctions à plusieurs variables.
Maintenant quelle sont les méthodes pour trouver la limite d'une fonction de deux variables en un point?
Il y a de multiples façons de s'approcher d'un point dans
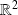 , donc il faut trouver une limite valable quelque soit la façons de s'approcher du point considéré.
, donc il faut trouver une limite valable quelque soit la façons de s'approcher du point considéré.
Calcul de la limite en (0, 0)
Deux techniques possibles :
Passage en coordonnées polaires :
Posons
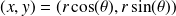 , ou
, ou
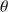 contrôle la direction, et donc
contrôle la direction, et donc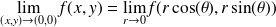 .
.Changement de variable (y=t x) :
Posons
 , ou
, ou
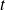 contrôle la direction, et donc
contrôle la direction, et donc
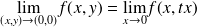 .
.
Remarque :
Soit la limite
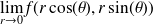 , ou
, ou
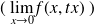 on a
on a
Si la limite existe et si elle ne dépend pas de la variable
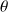 ( ou
( ou
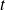 ), alors cette limite est la limite de
), alors cette limite est la limite de
 au point
au point
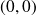 .
.Si la limite n'existe pas (ou la limite n'est pas finie), alors la limite de
 au point
au point
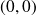 n'existe pas.
n'existe pas.Si la limite dépend de
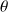 ( ou
( ou
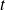 ), alors
), alors
 n'a pas de limite au point
n'a pas de limite au point
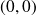 .
.Si la limite existe alors elle est unique.
Exemple :
Calculons les limites en point
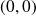 des fonctions suivantes :
des fonctions suivantes :
Soit
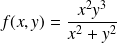
Posons
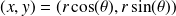 , on trouve
, on trouve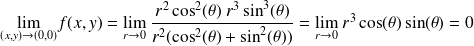 .
.Soit
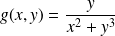
Posons
 , on trouve
, on trouve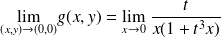 n'est pas finie donc cette limite n'existe pas.
n'est pas finie donc cette limite n'existe pas.Soit
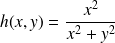
Posons
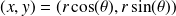 , on trouve
, on trouve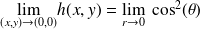 n'existe pas car elle est dépend de
n'existe pas car elle est dépend de
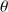 .
.
2. Calcul de la limite ailleurs qu'en (0, 0)
Dans tous ces cas on change la variable en
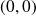 , puis on applique la règle de calcul de la limite à
, puis on applique la règle de calcul de la limite à
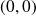 .
.
Limite en
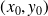 : on pose
: on pose
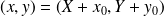 .
.Limite en
 : on pose
: on pose
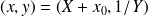 .
.Limite en
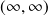 : on pose
: on pose
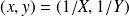 .
.
Voyons un exemple de chaque cas.
Exemple :
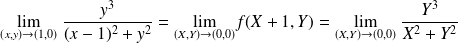 ,
,on pose
 , alors
, alors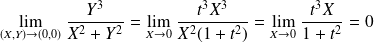 .
.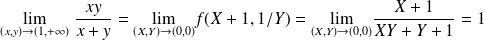 .
.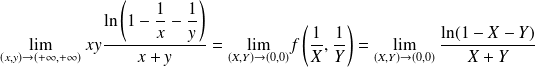 ,
,on pose
 , alors
, alors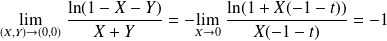 . Car
. Car
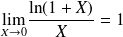 .
.
Fonctions continues
Définition :
Soit
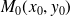 un point de
un point de
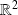 . On dit que la fonction
. On dit que la fonction
 est continue au point
est continue au point
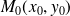 si :
si :
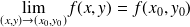 .
.
Exemple :
La fonction
 définie sur
définie sur
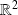 par
par
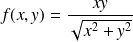 si
si
 et
et
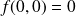 est-elle continue en
est-elle continue en
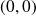 ?
?
Posons
 , on obtient
, on obtient
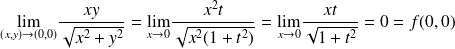 .
.
Donc
 est continue en
est continue en
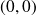 .
.
Dérivées partielles
Dérivées partielles d'ordre 1
Définition :
Soient
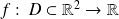 et
et
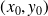 un point de
un point de
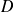 .
.
Si la fonction d'une variable
 (resp
(resp
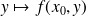 ) est dérivable en
) est dérivable en
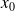 (resp est dérivable en
(resp est dérivable en
 )
)on dit que
 admet une dérivée partielle d'ordre 1 par rapport à
admet une dérivée partielle d'ordre 1 par rapport à
 (resp par rapport à
(resp par rapport à
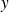 ) en
) en
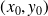 , et on note
, et on note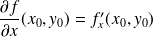 (resp
(resp
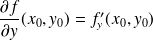 .
.Si pour tout élément
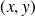 de
de
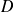
 admet une dérivée partielle d'ordre 1 par rapport à
admet une dérivée partielle d'ordre 1 par rapport à
 (resp par rapport à
(resp par rapport à
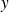 ) notées
) notées
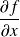 et
et
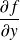 ou bien
ou bien
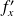 et
et
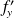 .
.
Méthode :
Pour calculer une dérivée partielle par rapport à une variable, il suffit de dériver par rapport à cette variable en considérant les autres variables comme des constantes.
Exemple :
Soit
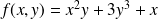 , on a
, on a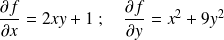 .
.Soit
 , on a
, on a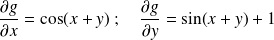 .
.Soit
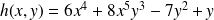 , on a
, on a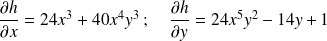 .
.
Dérivées partielles d'ordre 2
Définition :
Une fonction à deux variables
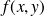 admet des dérivées partielles d'ordre 2 si deux dérivées partielles d'ordre 1 admettent elles-mêmes des dérivées partielles d'ordre 1 par rapport à
admet des dérivées partielles d'ordre 2 si deux dérivées partielles d'ordre 1 admettent elles-mêmes des dérivées partielles d'ordre 1 par rapport à
 et à
et à
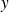 . On note
. On note
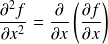 .
.
 .
.
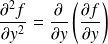 .
.
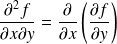 .
.
Exemple :
Pour la fonction
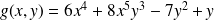 de l'exemple précédent, on a
de l'exemple précédent, on a
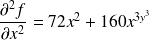 .
.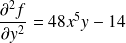 .
.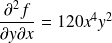 .
.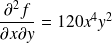 .
.
Extremums d'une fonction de deux variables
Définition :
On dit que la fonction
 admet un maximum local au point
admet un maximum local au point
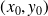 si il existe un voisinage
si il existe un voisinage
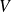 de
de
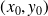 tel que pour tout point
tel que pour tout point
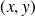 de
de
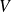 ,
,
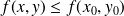 .
.On dit que la fonction
 admet un minimum local au point
admet un minimum local au point
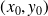 si il existe un voisinage
si il existe un voisinage
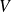 de
de
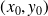 tel que pour tout point
tel que pour tout point
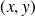 de
de
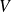 ,
,
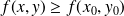 .
.On dit qu'une fonction
 admet un extremum local en un point donnée si elle a en ce point soit un maximum local soit un minimum local.
admet un extremum local en un point donnée si elle a en ce point soit un maximum local soit un minimum local.
Définition :
Soit
 une fonction de deux variables
une fonction de deux variables
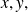 et
et
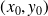 un point de
un point de
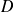 . On dit que
. On dit que
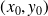 est un point critique de
est un point critique de
 si la dérivées partielles d'ordre 1 de
si la dérivées partielles d'ordre 1 de
 sont égales à
sont égales à
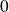 en ce point
en ce point
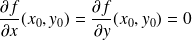 .
.
Fondamental : Théorème
Fondamental : Théorème
Soit
 une fonction de deux variables
une fonction de deux variables
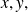 et
et
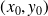 un point critique de
un point critique de
 , on note :
, on note :
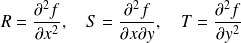
Si
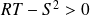 , alors
, alors
 admet un extremum en
admet un extremum en
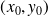 , un maximum si
, un maximum si
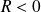 et un minimum si
et un minimum si
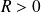 .
.Si
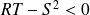 , alors
, alors
 il n'y a pas d'extremum en ce point.
il n'y a pas d'extremum en ce point.Si
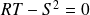 , alors on ne peut pas conclure.
, alors on ne peut pas conclure.
Méthode :
Pour calculer les extremums d'une fonction
 :
:
Trouver les points critiques de
 , ce qui revient à résoudre le système de deux équations à deux inconnues
, ce qui revient à résoudre le système de deux équations à deux inconnues
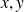 .
.Pour chacun des points trouvés, calculer
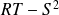 , puis conclure à l'aide du théorème précédent.
, puis conclure à l'aide du théorème précédent.
Exemple :
Déterminer les extremums de la fonction
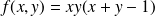 .
.
Points critiques :
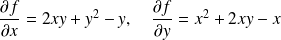 .
.Les points critiques sont solutions du système
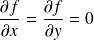 .
.On a
 admet
admet
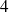 points critiques
points critiques
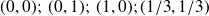 .
.Appliquons le Théorème précédente en ces points :
Les dérivées partielles secondes de
 sont:
sont: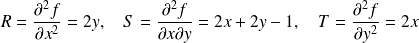 .
.En
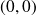 ;
;
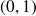 et
et
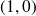 on a:
on a:
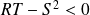 Donc,
Donc,
 n'admet pas d'extremum local de ces trois points.
n'admet pas d'extremum local de ces trois points.En
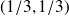 on a :
on a :
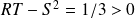 , Comme
, Comme
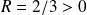 , alors
, alors
 admet un minimum local en
admet un minimum local en
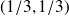 .
.