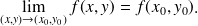Fonctions à deux variables
Définition :
Une fonction à deux variables est une application
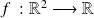 .
.
Exemple :
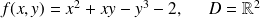 .
.
Définition :
Le
domaine de définition d'une fonction[1]
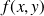 , noté
, noté
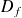 , est l'ensemble
, est l'ensemble
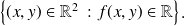
Pour déterminer
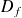 on passe par les étapes suivantes :
on passe par les étapes suivantes :
1) Écriture du domaine.
2) Détermination des frontières.
3) Représentation graphique et détermination des régions qui constituent
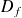 en utilisant des points particuliers situés dans les régions.
en utilisant des points particuliers situés dans les régions.
Exemple :
Soit
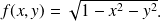
1)
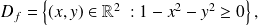
2) Déterminations des frontières
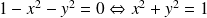
cercle de centre
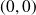 et de rayon
et de rayon
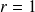
3) Le cercle divise le plan en deux régions, prenons deux points quelconques de ces deux régions.
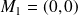 et
et
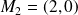
Pour
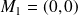 on a
on a
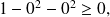
Pour
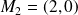 on a
on a
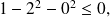
Donc
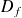 est le disque fermé.
est le disque fermé.
Limite et continuité
Limite en (0,0) :
Pour calculer la limite d'une fonction à deux variables
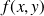 lorsque
lorsque
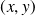 tend vers
tend vers
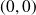 , deux techniques peuvent être utilisées :
, deux techniques peuvent être utilisées :
-Le changement de variable en coordonnées polaires :
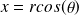 ,
,
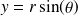 , ou
, ou
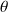 contrôle la direction et donc :
contrôle la direction et donc :
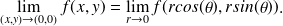
-Le changement de variable
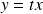 :
:
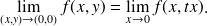
 Si la limite dépend de θ (ou t) cela veut dire que la limite n’existe pas.
Si la limite dépend de θ (ou t) cela veut dire que la limite n’existe pas.
limite en
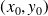
Pour calculer la limite d'une fonction lorsque
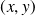 tend vers
tend vers
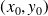 on procède comme suit :
on procède comme suit :
On pose
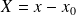 et
et
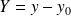
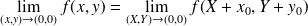 .
.
Limite en
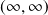 :
:
On pose
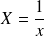 et
et
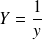
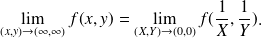
Continuité
La fonction f est dite continue en
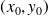 si :
si :