Points critiques et extremums
Définition :
Le point critique d'une fonction f à deux variables est le couple (x, y)qui vérifie
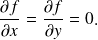
Définition :
Un point
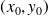est un maximum local de f, s'il existe un intervalle
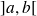tel que,
,
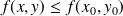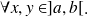
Définition :
Un point
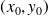est un minimum local de f, s'il existe un intervalle
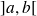tel que,
,
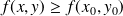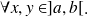
Théorème :
Si une fonction f admet un minimum ou un maximum local au point (x, y), alors ce point est un point critique.
Théorème :
Soit
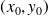un point critique d'une fonction à deux variables f, on note
,
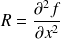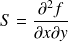
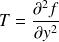et
.
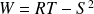Alors
1) Si en
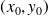on a
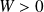, f admet en
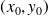un maximum si
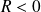et un minimum si
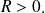
2) Si en
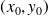on a
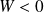, f n'admet pas d'extremum en
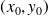. On parle de point selle.
3) Si en
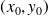on a
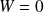, on ne peut pas conclure.
