Équation de Lagrange
Pour étudier le mouvement oscillatoire d'un système mécanique (connaître sa nature) on cherche à établir les équations mathématiques (différentielles) qui régissent le mouvement, il est nécessaire dans un premier temps de repérer sa position, grâce à un système d'axes dans l'espace.
L'équation différentiel du mouvement peut être déterminer par plusieurs méthodes :
Théorème de l'énergie mécanique (l'énergie mécanique est conservée.
Théorème de moment cinétique.
L'équation de Lagrange.
La méthode de Lagrange est apparu comme un moyen plus efficace (les calculs sont plus rapide) quelque soit la difficulté du système considéré pour l'obtention des équations du mouvement.
Cas des systèmes conservatifs
Un système est conservatif lorsqu'il n'y a pas d'échange d'énergie entre lui et l'extérieure. C'est à dire qu'il ne subit aucune force de frottement (perte) ou force d'excitation (entretient).
L'énergie totale d'un système conservatif est constante au cours du temps :
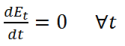
Cette équation de conservation donne l'équation différentielle des systèmes conservés (sans amortissement).
La méthode de Lagrange est une des méthodes qui permet de caractériser un mouvement par une formulation Lagrangienne qui nous produit un système d'équations différentielles associé au mouvement.
L'énergie totale d'un système mécanique est la composition des énergies cinétiques et potentielles :
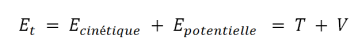
On définit une fonction mathématique (dont les variables sont les coordonnées généralisées) appelée fonction de Lagrange L ou "Lagrangien" donnée par :
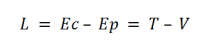
Pour un système conservatif les n équations du mouvement sont données par :
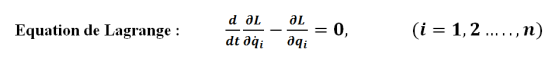
n : nombre de degrés de liberté
Dans le cas d'une translation suivant ‘x', l'équation s'écrit :
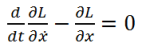
Dans le cas d'une rotation avec un angle θ, l'équation s'écrit :
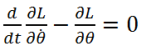
Nombre de degré de liberté
Le nombre minimal des coordonnées indépendantes nécessaires pour étudier un système vibratoire.
n = nombre de degrés de liberté = nombre de coordonnés généralisés = le nombre des équations différentiels
Les coordonnées généralisées
Les coordonnées généralisées sont des variables indépendantes, nécessaires et suffisantes pour décrire le même système mécanique à tout instant. Elles représentent les écarts par rapport à la position d'équilibre. qi avec i=1.........n. n : est le nombre de DDL[2]
Indépendantes : ne présentent aucune relation mathématique entre les coordonnées.
Nombre de coordonnés généralisés = Nombre de coordonnés - Nombre de relations entre ces coordonnés.
Exemple :
Le pendule simple :
connaître la position de la masse m dans chaque instant.
Deux coordonnées (x,y =2).
Par la connaissance d'une seule coordonnée x ou y, car elles sont liées par la relation : x2+y2=L2
n=2-1=1 degré de liberté
Exemple :
Le système masse-ressort
Pour connaître la position de la masse dans chaque instant, il faut connaître seulement l'abscisse x, une seule coordonnée, alors le système est à un degré de liberté
Exemple :
Deux masses et deux ressorts
Pour connaître les positions des masses m1 et m2 dans chaque instant il faut connaître les abscisses x1 et x2 (les deux coordonnées sont indépendantes), l'étude de ce système nécessite deux coordonnées donc le système est à deux degrés de liberté.
n =1 un système à un degré de liberté
n=2 un système à deux degré de liberté
Cas des forces de frottement dépendant de la vitesse
En réalité les systèmes sont soumis naturellement à des frottements [ 4[3]]. Lorsqu'un système oscillatoire est soumis à des forces de frottement fluide de la forme :
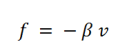
β = coefficient d'amortissement visqueux
On montre que l'on obtient les n équations du mouvement de ce système non conservatif grâce aux :
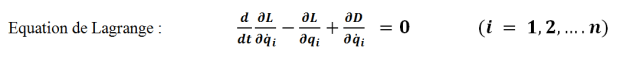
Avec L = La fonction Lagrangien ; n = nombre de degré de liberté
Et D = La fonction dissipation définit égale à la demi-puissance dissipée
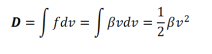
Cas d'une force extérieure dépendant du temps
Lorsqu'un système oscillatoire en plus d'être soumis à des forces de frottement qui dérivent d'une fonction dissipation D, est excité (entretenu) par une force extérieure dépendant du temps F (t)
On montre que l'on obtient les n équations du mouvement de ce système non conservatif grâce aux :
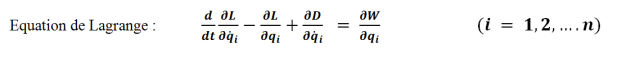
Avec :
L : fonction Lagrangien
D : fonction dissipation = 1/2 β v2
W: travail de la force d'excitation = ∫F dx=F






