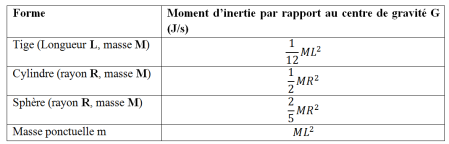
Formules usuelles
Un ressort se déforme au cours du mouvement, il n'y a pas de mouvement de masse, donc un ressort n'a pas d'énergie cinétique. (d'ailleurs on ne donne pas la masse d'un ressort dans les exercices).
La déformation d'un ressort est soit un allongement (ressort plus long) soit une compression (ressort plus court) par rapport à sa longueur à vide.
La force de rappel d'un ressort sur une masse est toujours négatif (car agit toujours dans le sens contraire de la déformation)
Ressort équivalant
Dans le cas de la présence de plusieurs ressorts, on procède par le calcul de raideur équivalent. Les raideurs sont liées soit en série ou en parallèle (opposition).

Ressorts en parallèle
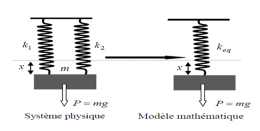
La constante de raideur du ressort équivalent est donnée par la relation suivante :keq=(k1+k2 )
Si le système est constitué de plusieurs ressorts en parallèles, alors la constante de la raideur du ressort équivalent est donnée par :
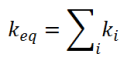
ressorts en série
la suspension de la masse m à l'extrémité libre des deux ressorts (k1 et k2) cause des allongements x1 et x2 dans k1 et k2 respectivement.
L'allongement total : xt=x1+x2
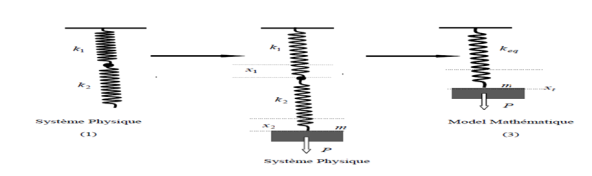
La constante de raideur du ressort équivalent est donnée par la relation suivante :
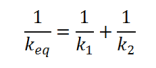
Dans le cas général ou le système est constitué de plusieurs ressorts en série :
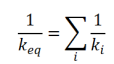
Toute masse « m » animée d'un mouvement de translation avec une vitesse v possède une énergie cinétique :
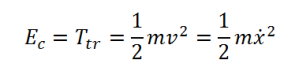
L'énergie cinétique de rotation d'un corps de moment d'inertie I/∆ est :
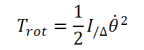
I/∆ : est le moment d'inertie par rapport aux point de l'axe de rotation.
L'énergie potentielle d'une masse dans un champ gravitationnel (L'énergie potentielle gravitationnel) :
Vmasse = mgh [assention d' une hauteur h]
Vmasse = -mgh [descente d' une hauteur h]
h : hauteur par rapport au sol
L'énergie potentielle d'un ressort de raideur k lors d'une déformation x est (L'énergie potentielle élastique) :
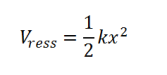
Rappel :
Moment d'inertie