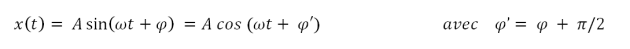Oscillations libres non amortis
Un système qui oscille en absence de toute force d'excitation, et des forces de frottement est appelé oscillateur libre non amorti (harmonique) où l'amplitude reste constante.
Dans les cas simples, le mouvement oscillant est décrit par une fonction sinusoïdale ; soit :
C'est aussi l'équation d'un mouvement harmonique sinusoïdale MHS[1] du type le plus simple des mouvements périodiques
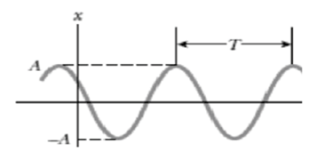
x(t) : est l'élongation (ou la position), à l'instant t, l'élongation maximale ou l'amplitude du mouvement varie entre –A et +A.
φ : La phase initiale à l'instant t=0.
(ωt+φ) : La phase instantanée à l'instant t, exprimée en radian.
Calcul de la vitesse d'un mouvement rectiligne sinusoïdal :
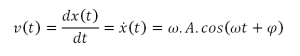
Il y a un déphasage constant de π/2 entre l'élongation et la vitesse. x(t) et v(t) sont en quadrature de phase.
Calcul de l'accélération d'un mouvement rectiligne sinusoïdal :
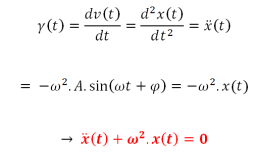
On obtient une équation différentielle linéaire du second ordre à coefficients constants sans second membre, caractéristique de ce type de mouvement.
Alors tout mouvement rectiligne vérifiant une équation différentielle linéaire du type :
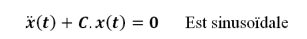
Avec C constante > 0, C = ω2
On notera : ω0 = √C pulsation propre du MHS (mouvement harmonique sinusoïdal).
Un mouvement oscillatoire est dit rectiligne à un degré de liberté lorsqu'il a lieu dans une direction unique de l'espace, et la connaissance d'une seule variable de position suffit pour connaître sa position.