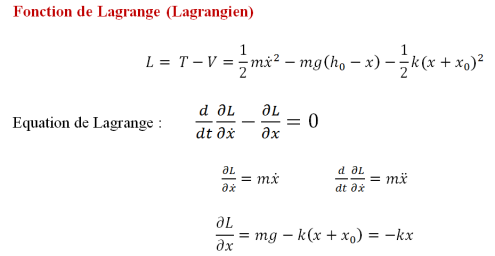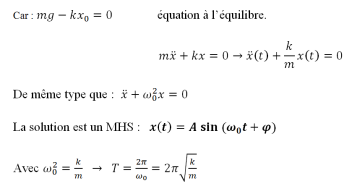Mouvement oscillatoire de translation (le système masse-ressort)
La méthode de Newton
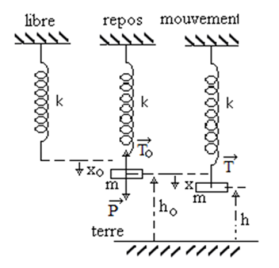
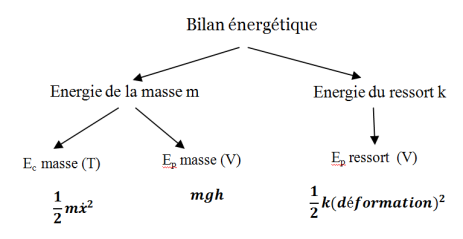
C'est un système conservatif à un degré de liberté x.
Ressort de raideur k (coefficient d'élasticité), sans masse.
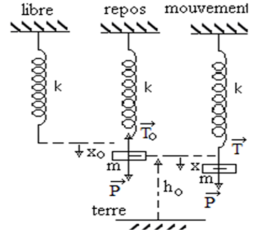
Masse m au repos
Le ressort est allongé de x0 ;
x0 : est une déformation statique.
C'est une situation d'équilibre donc pas de mouvement.
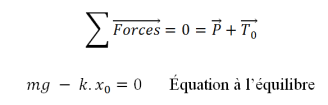
Masse m est écarté de x puis lâchée
Nous avons donc une oscillation ;
x : déformation dynamique
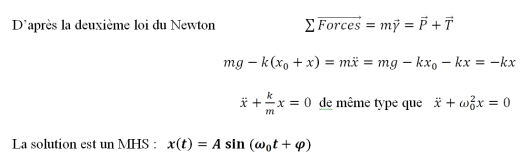
Méthode de Lagrange
Le système masse-ressort a un degré de liberté. Il est libre (aucune force extérieure) et conservatif (non amorti).