Mouvement oscillatoire de rotation (le pendule simple)
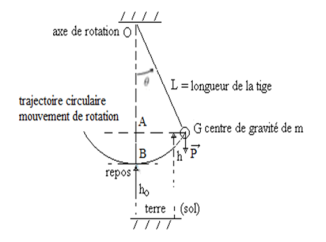
La masse m est ponctuelle, animée d'un mouvement oscillatoire de rotation avec une vitesse angulaire dθ/dt par rapport à O distant de L. La tige est considérée sans masse. C'est un système conservatif à un degré de liberté θ. Le pendule est simple.
La masse m possède un moment d'inertie J = mL2 donc une énergie cinétique de rotation :
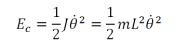
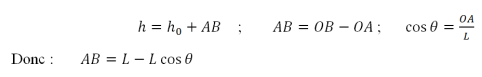
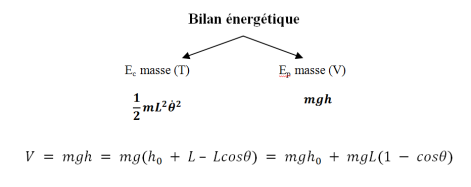
La fonction de Lagrange (Lagrangien):
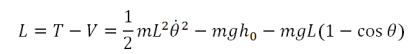
Équation de Lagrange:
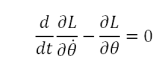
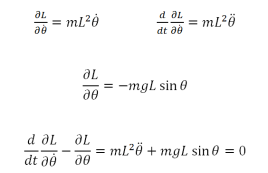
Cette formule est non linéaire nous devons faire des approximations. Dans le cas des petites oscillations (θ << 10°) ou bien (θ en rad << 1) on peut faire l'approximation suivante :
sinθ≈θ ; cosθ ≈ 1

De même type que :
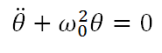
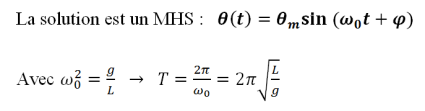
Remarque :
Le moment d'inertie dans un système qui fait un mouvement de rotation est équivalent à la masse dans un système faisant un mouvement de translation.
Si le système est constitué de deux masses distantes (les masses sont éloignées) le moment d'inertie est donné par : I=m1 r12+m2 r22






