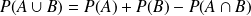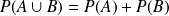Calcul de probabilités
Définition : Probabilité
La probabilité d'un événement
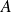de l'univers
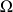est un nombre compris entre
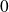et
appelé probabilité de A, noté P(A), tel que :
.
.
.
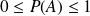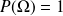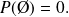
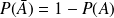Fondamental :
Fondamental :
Quand les événements élémentaires sont équiprobables[2], la probabilité d'un événement
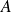est:
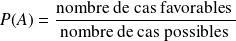
Exemple :
On lance un dé cubique
Événement
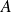: "avoir
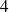". Les cas sont équiprobables.Nombre de cas favorables est
. Nombre de cas possibles est
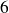. Donc
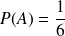.Événement
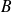: "ne pas avoir
".
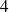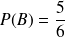.Événement
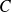: "avoir un nombre pair".
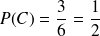.Événement
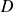: "avoir un nombre pair ou impair".On pose
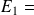"nombre pair",
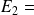"nombre impair",
.
.
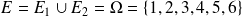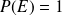Définition : Probabilité conditionnelle
Soit
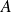et
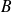deux événements avec
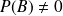. La probabilité conditionnelle (probabilité que de
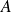se réalise sachant que
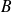est réalisé) défini par :
.
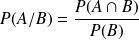Définition : Événements indépendants
On dit que l'événement
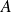est indépendant de
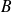si
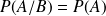ce qui est équivalent à
.
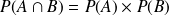Attention :
Ne pas confondre indépendance et incompatibilité, si
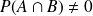les deux événements sont compatibles, ils pourront être dépendants ou indépendants.
Exemple :
Les événements
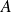et
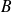décrivant la composition de l'amphithéâtre sont compatibles et dépendants.
