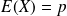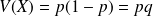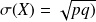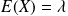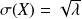Lois statistiques et application bio statistiques
Principales lois de variables discrètes
Loi de Bernoulli
Définition :
On appelle épreuve de Bernoulli toute expérience aléatoire modélisée par un univers
qui ne contient que deux éventualités baptisées : succès (auquel on associe la valeur
de probabilité
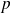) et échec (au quel on associe la valeur
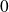de probabilité
).
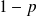On appelle " loi de probabilité de Bernoulli " (ou "loi de Bernoulli "), noté par
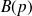la loi de probabilité associée à une épreuve de Bernoulli.
une v.a discrète suit une loi de Bernoulli de paramètre
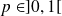, si
.
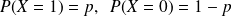Paramètres caractéristiques d'une loi de Bernoulli
Loi binomiale
Définition :
Soient
variables aléatoires
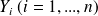de Bernoulli indépendantes et de même
paramètre
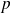alors
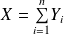est une variable aléatoire qui suit une loi binomiale de paramètres
et
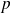. on note
.
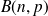Pour tout entier naturel
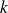inférieur ou égal à
, on a :
.
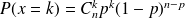Paramètres caractéristiques d'une loi Binomiale
,
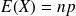
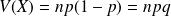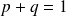
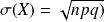
Exemple :
Soit une famille de
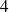enfants dont les parents sont porteurs d'un gène d'une maladie héréditaire. La variable aléatoire
: " nombre d'enfants atteints de cette maladie dans la famille " est discrète à cinq réalisations possibles
.
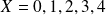On a
suit
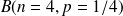alors
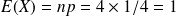
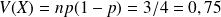
On peut calculer les différentes probabilités
.
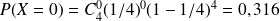
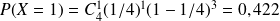
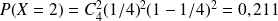
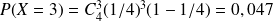
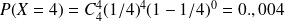Loi de poisson
Définition :
On dit qu'une v.a
, à valeurs dans
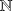suit une loi de poisson de paramètre
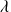( on note
suit
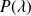) si sa loi de probabilité est
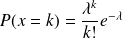où
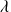est un réel strictement positif.
Paramètres caractéristiques d'une loi de Poisson
Principales lois d'une variable aléatoire continue
Loi normale
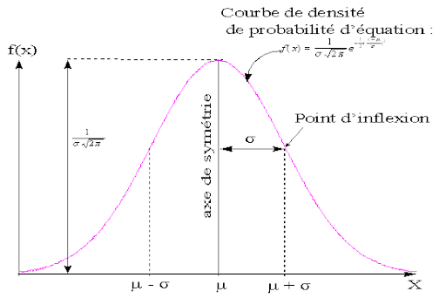
La loi normale est la loi la plus connue des probabilités pour les variables aléatoire continues., parfois sous le vocable loi de Laplace-Gauss et caractérisée par une célèbre "courbe en cloche".
Définition :
suit une loi normale d'espérance
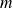ou
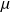et d'écart type
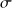si sa densité est donnée par :
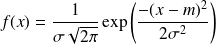où
est un réel ,on dit que
suit une loi
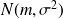ou
.
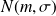Dans le cas particulier où
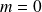et
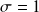, on dit que
suit une loi normale centrée réduite et sa densité est définie par:
.
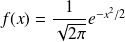La fonction de répartition
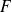de la loi normale est donnée par:
.
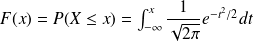Fondamental :
Soit
une v.a de loi normale
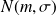et
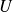la v.a définie par :
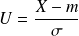, alors
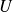suit une loi normale centrée réduite
.
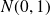Propriété de la fonction de répartition
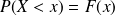
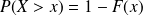
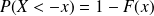
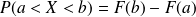
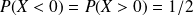
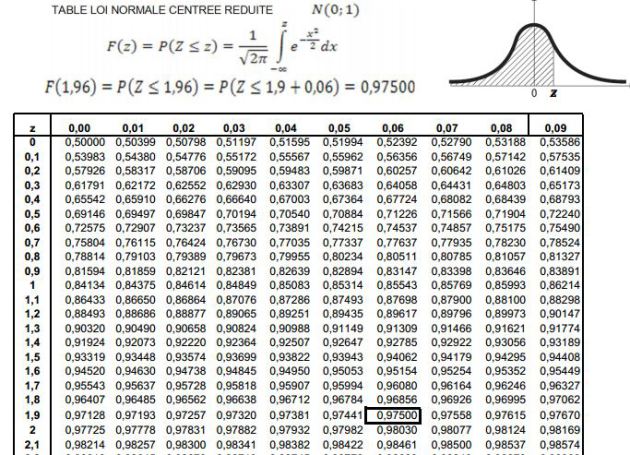
Exemple : Exemple d'utilisation de la table
Calculons à l'aide de la table de la loi normale centrée réduite les probabilités suivantes : (
suit la loi
)
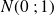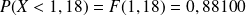. En effet, d'après la table, on a
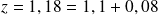, alors sa probabilité est intersection entre la colonne de chiffre
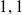et la ligne de chiffre
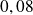qui est vaut
.
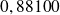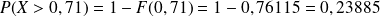. (On applique la même méthode).
.
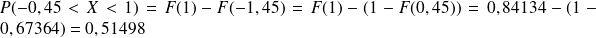Calculons
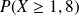sachant que
suit une loi normale
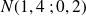.Il faut centré et réduite la variable
. On pose
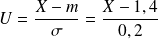, alors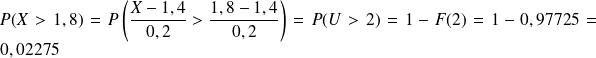
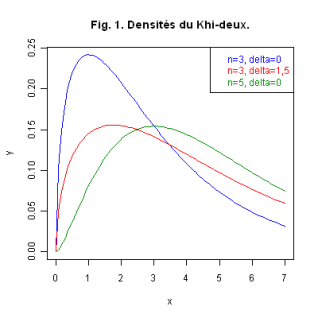
Loi du Khi-Deux (Χ2 ) ou loi de Pearson
Définition :
On considère
v.a
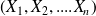indépendantes suivant toutes la loi normale
.
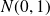La variable aléatoire
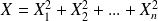suit une loi du Khi-deux à
degré de liberté, notée
.
Sa Densité de probabilité
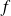est définie sur
:
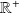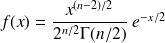, avec
.
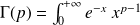Espérance mathématique et variance de
:
.
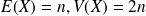