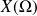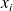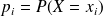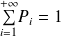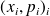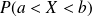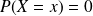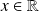Variables aléatoires
1. Variables aléatoires discrètes
Définition :
Définition :
La fonction de répartition associée à la variable aléatoire
est la fonction notée
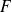ou
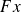définie de
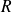dans l'intervalle
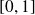par
.
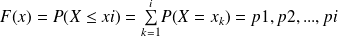Pour tous réel,
et
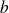on a
.
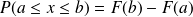Remarque :
On peut rapprocher les effectifs cumulés croissants calculés sur une série statistique avec la fonction de répartition.
Paramètres caractéristiques
Espérance mathématique
L'espérance mathématique, noté
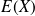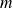, ou
ou
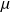, d'une v.a
est donnée par :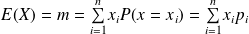
.Variance
La variance, noté
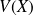de la v.a
est donnée par une des deux relations suivantes :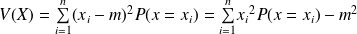
.Écart type
L'écart type
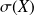d'une v.a
est donnée par :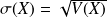
.L'écart type donne la dispersion des valeurs de la variable aléatoire
L'écart type donne la dispersion des valeurs de la variable aléatoire
par rapport à l'espérance mathématique
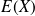.Moment d'ordre
On appelle moment d'ordre
l'espérance mathématique de la variable aléatoire
.
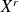
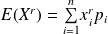Complément : Propriétés de l'espérance et de la variance
Soient
et
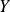deux variables aléatoires et
et
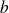sont des nombres réels
.
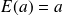
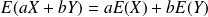
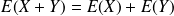
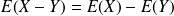
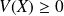
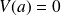
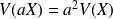
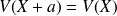Remarque :
Si
et
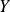sont indépendantes alors
.
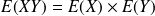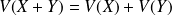, la réciproque est fausse.
Exemple :
la variable
associée à l'événement " un individu développe t-il une allergie " a deux réalisations possibles
" l'individu développe une allergie " codée généralement par
état associé au succès"l'individu ne développe pas une allergie " codée par
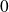, état associé à l'échec.
Calculons les paramètres caractéristiques
.
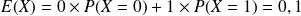
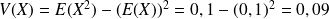
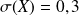
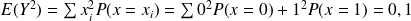2. Variable aléatoire continue
Définition :
Exemple :
Le poids d'un individu est une variable aléatoire qui peut prendre une infinité de valeurs dans un intervalle de
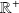
Définition :
Une v.a continue peut être défini par sa fonction de répartition
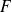ou
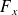, définie par
.
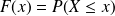Quelques propriétés de la fonction de répartition
Pour tout réel
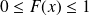
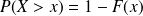
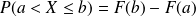pour tous réel a et b tel que
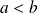
La fonction
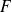est croissante et continue sur
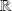
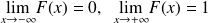
Définition : Fonction de densité de probabilité
On appelle densité de probabilité toute fonction
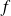définie continue ( sauf éventuellement en un nombre fini de points ) et positive sur
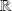et telle que :
.
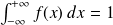Soit
une v.a. continue de fonction de répartition
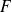alors : pour tout réel
, la fonction
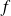définie sur par
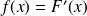est une densité de probabilité de
.
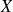Paramètres caractéristiques
Espérance mathématique
L'espérance mathématique d'une variable continue
est le nombre réel (si il existe ) , noté
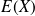défini par :
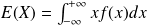.Variance
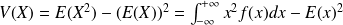.Écart-type
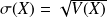.Moments
Le moment d'ordre
d'une variable aléatoire continue est défini par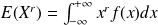
.
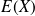est le moment d'ordre
.
Exemple :
La fonction
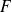définie par 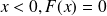si
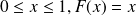; si
; si
.
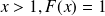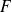ainsi défini remplit les conditions d'une fonction de répartition d'une variable aléatoire.
La fonction de densité de probabilité de la variable aléatoire décrite par la fonction de répartition
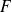es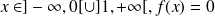t si
et si
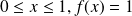
Cette fonction décrit une variable aléatoire qui peut prendre toutes les valeurs réelles comprises entre
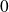et
.
.
.
.
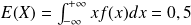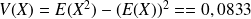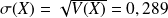