Généralités
C'est quoi une fonction ?
[1]Une fonction est une relation qui associe chaque élément d' un ensemble appelé ensemble de départ à un élément d'un autre ensemble appelé ensemble d'arrivée
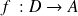
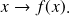
Exemple :
Soient
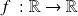
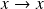
et
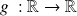
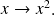
des fonctions réelles.
Définition : La fonction f est dite :
Paire si et seulement si
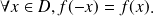
Impaire si et seulement si
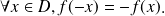
Périodique si et seulement si
.
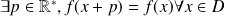Définition : Fonction bijective
Une fonction
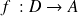est dite bijective si pour tout
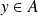l'équation
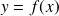possède une solution unique.
Exemple :
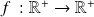
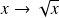
est une fonction bijective.
Définition : Fonctions réciproques
Si
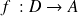est une fonction bijective, alors il existe une fonction réciproque notée
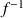telle que
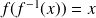et
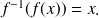
Exemple :
Soit
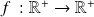
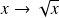une fonction bijective, sa fonction réciproque est
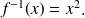
Fonctions trigonométriques réciproques
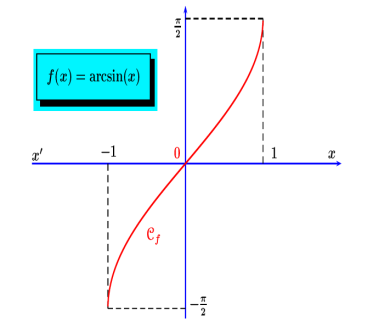
Fonction arcsinus :
la fonction
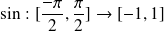est bijective sur
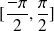, alors il existe une fonction réciproque appelé
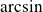définie sur
.
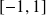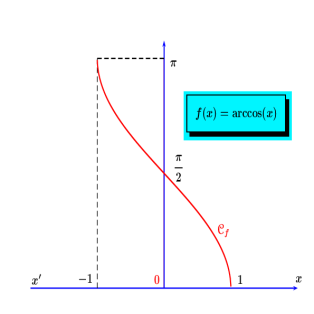
Informations[2]Fonction arc cosinus :
la fonction
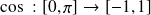est bijective sur
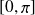, alors il existe une fonction réciproque appelée arccosinus et notée
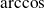est définie sur
.
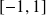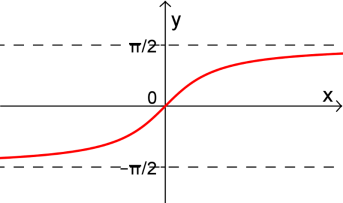
Fonction arc tangente :
La fonction
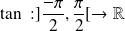est bijective alors il existe une fonction réciproque appelée arc tangente et notée
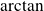est définie sur
