Dérivation
Définition :
Soit
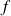 une fonction définie sur un intervalle
une fonction définie sur un intervalle
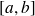 . On dit que f est dérivable sur
. On dit que f est dérivable sur
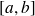 si
si
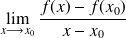 existe et est finie.
existe et est finie.
Cette limite s'appelle la dérivée de f en
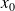 , on la note
, on la note
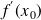 .
.
Exemple :
La dérivée en
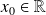 de la fonction
de la fonction
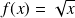 est
est
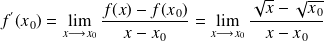
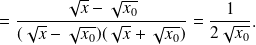
Propriétés :
Soient
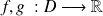 deux fonctions dérivables alors on a :
deux fonctions dérivables alors on a :
1- Linéarité :
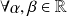 :
:
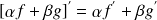 ;
;
2- Dérivée du produit de deux fonctions :
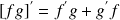 .
.
3- Dérivée du rapport de deux fonctions :
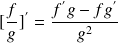 .
.
4- Dérivée de la composée de deux fonctions :
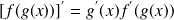 .
.
5- Puissance d'une fonction :
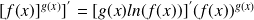 .
.
Théorème de Rolle
Soit
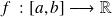 une fonction qui vérifie les conditions suivantes:
une fonction qui vérifie les conditions suivantes:
- f est continue sur
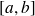 ,
,
- f est dérivable sur
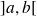 ,
,
-
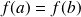 ,
,
alors il existe au moins un point c de
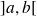 tel que
tel que
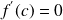 .
.
C'est à dire que f atteint en c un extremum local ( c'est à dire un maximum ou minimum local) dans
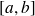 .
.
Définition :
On dit que f atteint en
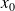 un maximum local s'il existe un intervalle I contenant
un maximum local s'il existe un intervalle I contenant
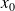 tel que pour tout élément x de I, on a
tel que pour tout élément x de I, on a
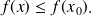
Définition :
On dit que f atteint en
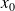 un minimum local s'il existe un intervalle I contenant
un minimum local s'il existe un intervalle I contenant
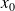 tel que pour tout élément x de I, on a
tel que pour tout élément x de I, on a
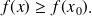
Définition :
On dit que
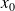 est un point critique de f si
est un point critique de f si
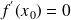 .
.
Règle de l'Hôpital :
Soient
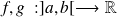 dérivables telles que
dérivables telles que
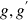 ne s'annulent pas sur
ne s'annulent pas sur
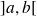 . De plus on suppose que
. De plus on suppose que
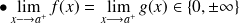
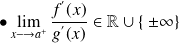
Alors
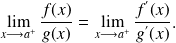
Tableau des dérivées







