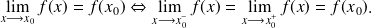Continuité
Définition :
Proposition :
Soient f et g deux fonctions continues en
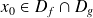 , alors :
, alors :
1)
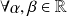 ,
,
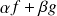 est continue en
est continue en
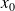 ;
;
2) Le produit
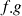 est continue en
est continue en
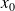 ;
;
3) Si
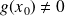 alors la fraction
alors la fraction
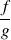 est continue en
est continue en
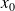 ;
;
4)
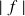 est continue en
est continue en
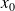 .
.
Théorème des valeurs intermédiaires :
Soit f une fonction définie sur un intervalle
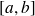 .
.
Si
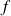 est une fonction continue sur
est une fonction continue sur
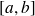 et
et
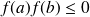 alors il existe au moins un point
alors il existe au moins un point
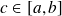 tel que
tel que
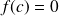 .
.
Exemple :
Soit
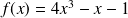 définie sur l'intervalle
définie sur l'intervalle
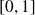 .
.
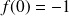

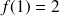

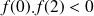 .
.
Alors il existe un
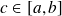 tel que
tel que
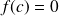 .
.