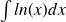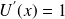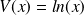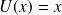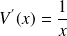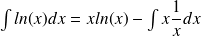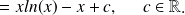Intégration
Définition :
On appelle primitive d'une fonction f définie sur un segment
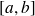 , toute fonction F définie et dérivable sur
, toute fonction F définie et dérivable sur
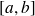 telle que
telle que
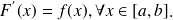
On écrit aussi
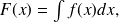 appelée une intégrale indéfinie de f.
appelée une intégrale indéfinie de f.
La quantité
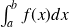 définie par
définie par
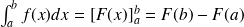 est appelée une intégrale définie de f.
est appelée une intégrale définie de f.
Propriétés de l'intégrales
Soient f et g deux fonctions intégrables sur [a,b] et
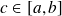 . Alors on a :
. Alors on a :
1)
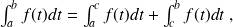
2)
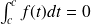 ,
,
3)
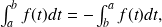
4)
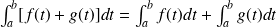
5)
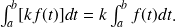
Techniques de calcul de primitives.
Intégration par partie (IPP[1])[1][1]
Proposition : Soient u et v deux fonctions dérivables sur
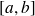 , on a :
, on a :
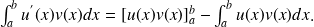
Exemple :
Changement de variable :
Soit
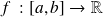 une fonction intégrable et
une fonction intégrable et
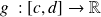 une fonction dérivable telle que
une fonction dérivable telle que
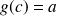 et
et
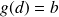 , alors
, alors
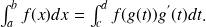
Exemple :
Calculer
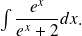
On pose
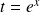 et donc
et donc
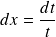
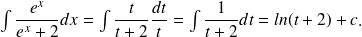
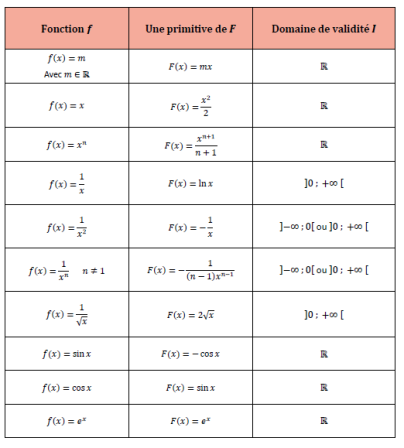
Tableau des primitives usuelles