Aperçu des sections

  • Généralités

    Tout replier Tout déplier

    Bienvenue à mon cours


    Le module Analyse 1 a pour objectif d’initier l’étudiant aux notions fondamentales de l’analyse mathématique. Il aborde l’étude des fonctions réelles d’une variable réelle, des limites, de la continuité et de la dérivabilité. Une attention particulière est accordée aux propriétés des suites réelles et à leur convergence. Le cours permet de développer la rigueur mathématique et les techniques de calcul indispensables pour les modules avancés. Il constitue une base essentielle pour la poursuite des études en mathématiques et disciplines connexes.


    1

  • Fiche de contact

    Enseignante de la matière : SEDDAR MANAL 
    Contact : manel.seddar@univ-tlemcen.dz
    Faculté : Faculté des Sciences
    Département : Mathématiques
    Filière : Licence Mathématiques et Informatique
    Niveau : L1
    Unité d’enseignement : Fondamentale
    Coefficient : 2
    Crédit : 4
    Volume horaire hebdomadaire : 3h (1h30 Cours + 1h 30 TD)

    Modalité du suivi :
    Lundi de 10h00 à 11h 30 (cours)

    mardi 14h à  15h30 (TD)

    Modalité d’évaluation :

    • Contrôle continu : 50%

    • Examen final : 40%

    Détail du Contrôle Continu :

    • 40% :Test 1 

    • 40% :Test 2 

    • 20% : Présence et participation

  • Objectifs de la matière

    La matière Analyse 1 vise à :

    • Comprendre les notions fondamentales liées aux suites réelles et à leur convergence.

    • Définir et maîtriser les limites et la continuité des fonctions réelles.

    • Appliquer les théorèmes essentiels de l’analyse pour étudier le comportement des fonctions.

    • Développer les techniques de dérivation et utiliser la dérivée pour analyser et résoudre des problèmes.


  • Préliminaire

    À travers ce premier cours, l’étudiant comprend :

    • Les notions de base sur les ensembles, intervalles, fonctions et valeur absolue.

    • Comment lire, interpréter et représenter graphiquement une fonction réelle.

    • Comment manipuler les premières notions nécessaires pour aborder les limites et la continuité.


  • Prérequis

    Pour bien suivre le contenu de la matière Analyse 1, l’apprenant doit avoir acquis certaines connaissances sur :

    • Les notions de base des fonctions réelles : opérations, graphiques, variations simples.

    • Les propriétés élémentaires des nombres réels : ordre, intervalles, valeur absolue.

    • Les notions fondamentales d’algèbre : équations, inéquations, factorisation.

    • Les manipulations simples de limites usuelles vues au lycée.


    • quiz icon
      Test à Prérequis
      Ouvert : mercredi 10 décembre 2025, 14:24
      Se termine : dimanche 28 décembre 2025, 14:24

  • Table de matières

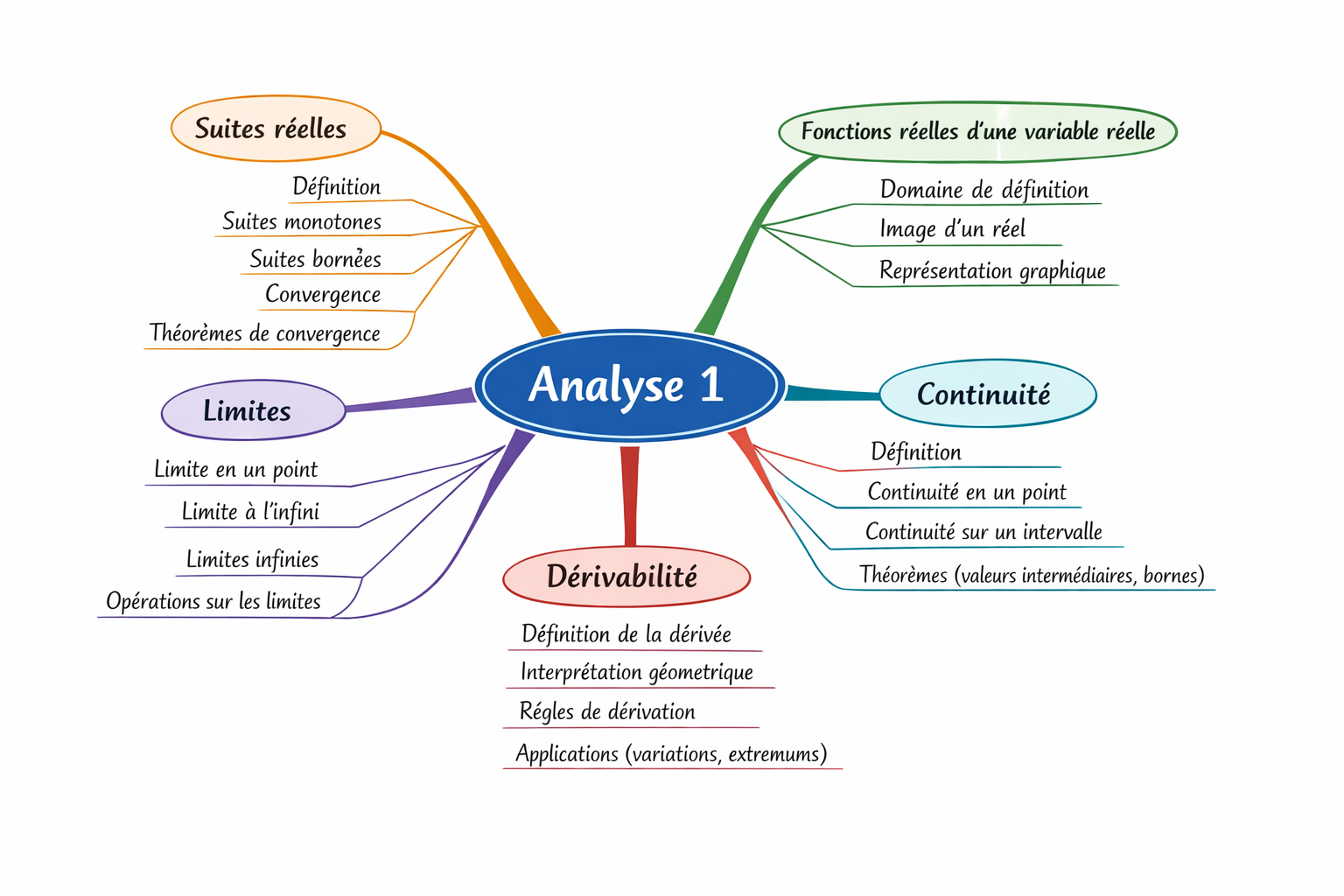
    Chapitres du module

    1. Suites et limites : convergence, divergence, théorèmes de base.

    2. Limites et continuité des fonctions : propriétés, théorèmes importants.

    3. Dérivabilité et applications : règles de dérivation, étude de fonctions.


  • Carte conceptuelle de la matière

    SEDDAR

  • Chapitre 01 :Suites et limites

  • Chapitre 02 :Limites et Continuité des Fonctions

  • Références bibliographiques

    • Jean-Marie Monier, Analyse – Cours complet avec 800 exercices corrigés, Dunod, 2013.

    • Sébastien Frachebourg, Analyse – Cours et exercices corrigés, Ellipses, 2018.

    • Patrick Dehornoy, Analyse – Tome 1 : Fonctions d’une variable réelle, Calvage & Mounet, 2014.

    • *Cours de Mathématiques de L1 – Analyse 1, Universités françaises (poly de cours : Paris-Saclay, Grenoble, Lyon…).

    • Robert Adams, Calculus – A Complete Course, Pearson, 2013.

    • Tom M. Apostol, Calculus, Volume 1, Wiley, 1967.

    • Serge Lang, A First Course in Calculus, Springer, 2005.

    • H. Cartan, Cours de Calcul Différentiel, Hermann, 1967.


  • Avis des étudiants

  • Section 11

  • Section 12