المتوسط الحسابي Arithmetic Mean
تعريف المتوسط الحسابي
يمكن تعريفه بأنه "عبارة عن حاصل قسمة مجموع قيم البيانات i على عددها n.
كما يُعرف بأنّه القيمة المركزية أو الوسطية لمجموعة مكوّنة من رقمين أو أكثر، ويمكن حسابه ببساطة من خلال الخطوات الآتية:
إيجاد مجموع البيانات المعطاة. إيجاد حاصل قسمة مجموع البيانات على عددها. يمكن التعبير عن الوسط الحسابي رياضيًا من خلال القانون الآتي: M= (x1+ x2+ x3+ ...xn)/ n حيث إنّ: M: الوسط الحسابي. x1، x2، x3، xn: هي قيم البيانات المعطاة. n: عدد القيم المعطاة.
خصائص المتوسط الحسابي
يتأثر بالقيم المتطرفة أو الشاذة؛
يستعمل في حالة المتغيرات الكمية القابلة للقياس؛
لا يمكن أن يكون لأي توزيع تكراري أكثر من وسط حسابي؛
أكثر مقاييس النزعة المركزية استخداما؛
مجموع انحرافات المتغير الإحصائي بالنسبة للمتوسط الحسابي تساوي الصفر؛
متوسط قيمة ثابتة يساوي تلك القيمة الثابتة.
حساب المتوسط الحسابي من البيانات الأولية
البيانات الأولية هي البيانات التي لا تكون علي شكل جداول تكرارية، وتكون البيانات غير مبوبة عندما يكون لقياسات المتغير المدروس نفس المستوى من الأهمية، وهذا النوع من أنواع الوسط الحسابي هو الأسهل لأنه لا يحتاج إلى جداول تكرارية كل ما يحتاج إليه هو حصر مجموع المشاهدات الموجودة وقسمتها على عدد هذه القيم .فإذا كانت لدينا القيم: X1,X2,.....Xn تمثل قيم ظاهرة ما فإن متوسط هذه القيم يحسب بالصيغة التالية:
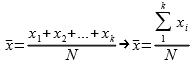
مثال :
تمثل السلسة التالية تطور إنتاج زيت الزيتون بالجزائر في الفترة 2012-2018
الموسم الزراعي | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|
الكمية المنتجة | 39,5 | 66 | 44 | 69,5 | 82 | 63 | 82,5 |
المطلوب: حساب متوسط الإنتاج.
الحل: البيانات غير مبوبة فإن:
Mean=Σxi/N=(39.5+66+....+82.5)/9=63.7857
معناه أن متوسط أو معدل إنتاج زيت الزيتون في الجزائر للفترة 2012-2018 بلغ 63.7857 ألف طن.
حساب المتوسط الحسابي من البيانات المبوبة
في حالة كان لدينا مجموعة من القيم ، ويوجد وسط هذه القيم مجموعه منها متساوية ، فبسهولة يمكن تجميع وتلخيص هذه القيم في جدول تكراري بسيط حسب القيم المكررة ،
في هذه الحالة تكون القيم المراد حساب متوسطها الحسابي ليست على نفس القدر من الأهمية، بل تختلف حسب عامل الترجيح. في هذه الحالة يتطلب الأمر استخدام صيغة أخرى تسمى صيغة المتوسط الحسابي المرجح، وفيها نميز حالتين:
حالة متغير كمي منفصل
إذا كانت القيم X1,X2...Xn تمثل قيم ظاهرة معينة. وكان n1,n2...nk تمثل التكرارات المقابلة لها. نستطيع حسب الوسط الحسابي لهذه القيم عن طريق جمع حواصل ضرب القيم في تكراراتها مقسوما على مجموع التكرارات . وتعطى علاقة المتوسط الحسابي بالصيغة التالية:
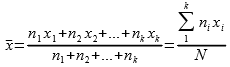
مثال :
البيانات التالية تمثل توزيع عائلات حي سكني معين حسب عدد الأطفال
عدد الأطفال Xi | 0 | 1 | 2 | 3 | 4 | Σ |
|---|---|---|---|---|---|---|
عدد العائلات ni | 5 | 20 | 35 | 25 | 15 | 100 |
المطلوب: إيجاد متوسط غرف عائلات الحي.
نضيف سطر ثالث للجدول السابق لحساب المجموع المرجح لهذه القيم كما يلي:
عدد الأطفال Xi | 0 | 1 | 2 | 3 | 4 | Σ |
|---|---|---|---|---|---|---|
عدد العائلات ni | 5 | 20 | 35 | 25 | 15 | 100 |
Xi*ni | 0 | 20 | 70 | 75 | 60 | 225 |
ومنه متوسط الغرف المملوكة هو2≈ 2,25=225/65= Σnixi/N
حالة متغير كمي متصل
في هذه الحالة يكون جدول التوزيع التكراري في شكل فئات عددها k، فإذا كانت من المعلوم أن القيم الأصلية، لا يمكن معرفتها من جدول التوزيع التكراري، حيث أن هذه القيم موضوعة في شكل فئات، ولذا يتم التعبير عن كل قيمة من القيم التي تقع داخل حدود الفئة بمركز هذه الفئة، ومن ثم يؤخذ في الاعتبار أن مركز الفئة هو القيمة التقديرية لكل مفردة تقع في هذه الفئة.
فإذا كانت K هي عدد الفئات، وكانت C1.C2.....,CK هي مراكز هذه الفئات وكانت تكراراتها n1,n2....nk على الترتيب، فإن الوسط الحسابي يحسب بالمعادلة التالية:
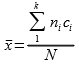
مثال :
لمعرفة ودراسة تطور مداخيل العائلات السنوية أخذت عينة من منطقة ما وبعد جمع كانت النتائج كما يلي:
الفئات | التكرار ni | مركز الفئة ci | ni*ci |
[125 -120[ | 10 | 122,5 | 1225 |
[130-125[ | 20 | 127,5 | 2550 |
[135-130[ | 38 | 132,5 | 5035 |
[140-135[ | 25 | 137,5 | 3437,5 |
[145-140[ | 7 | 142,5 | 997,5 |
المجموع | 100 | - | 13245 |
ومنه المتوسط الحسابي هو 132,45=13245/100= Σnici/N
وعليه متوسط مداخيل العائلات هو 132,45 وحدة نقدية.






