مقياس الإحصاء الوصفي

في التوزيع التكراري الاعتدالي وحيد المنوال تنطبق المقاييس الثلاث على بعضها في الشكل البياني لتأخذ نفس القيمة، حيث: المنوال=الوسيط=المتوسط الحسابي حيث تستعمل العلاقة للتحقق من التماثل التام للتوزيع كما في الشكل الموالي.

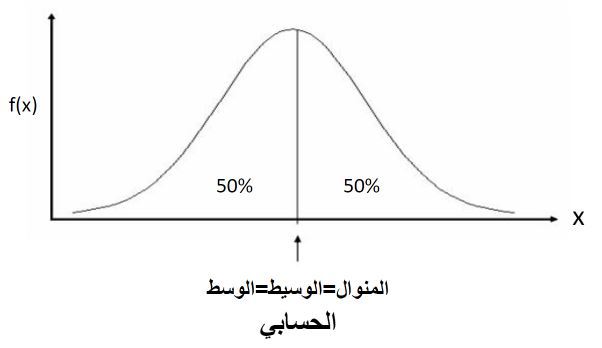
بينما في الشكل الموالي نجد أن هناك علاقة بين المتوسط الحسابي والوسيط والمنوال حيث المتوسط الحسابي< الوسيط < المنوال وذلك يعني أن التوزيع ذو التواء سالب ملتوي نحو اليسار.

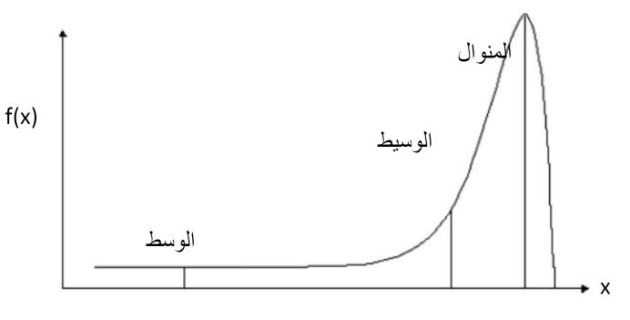
بينما في الشكل الموالي نجد أن المتوسط الحسابي< الوسيط <المنوال، وذلك يعني أن التوزيع ذو التواء موجب نحو اليمين, وفي كلتا الحالتين السابقتين فإن الوسيط يقع بين المتوسط الحسابي والمنوال في حين أن المتوسط الحسابي يقع دائما في اتجاه القيم الشاذة.

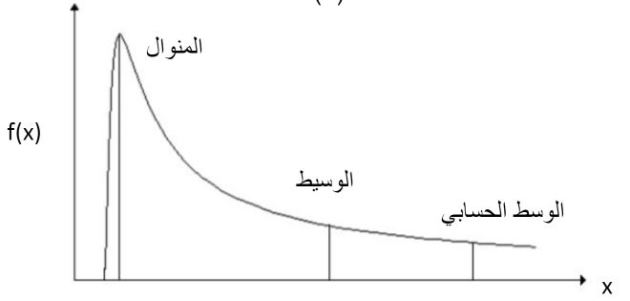
كما تلخص العلاقة التجريبية لبيرسون Pearson empirical relationship بين مقاييس النزعة المركزية والتي تتحقق في حالة المنحنيات التكرارية وحيدة المنوال وبسيطة الالتواء، وهي:

حيث يمكن حساب مقياس بدلالة من مقاييس النزعة المركزية في حالة توفر المقياسين الآخرين.