مقياس الإحصاء الوصفي

حل السلسلة رقم 3:

التمرين الأول:

1- حساب متوسط عدد أطفال العائلات

1.2 العدد الوسيط للأطفال:

نحسب أولا رتبة الوسيط:

تحديد الفئة الوسيطية

نحسب التكرار المتجمع المطلق الصاعد كما في الجدول أدناه.

نذهب مباشرة إلى سطر التكرار المتجمع الصاعد في الجدول السابق ثم نبحث عن المشاهدة التي تقابلها قيمة رتبة الوسيط 50 أو التي هي أكبر منها مباشرة في هذه الحالة 65. والمشاهدة التي تقابلها هي:

2.2 عدد الأطفال المتواجدين في أكبر عدد من العائلات

المنوال: قيمة المشاهدة التي يقابلها أكبر تكرار. من الجدول السابق أكبر تكرار مطلق هو 25 يقابلها قيمة

3. شكل التوزيع: نقارن بين قيمة المنوال والمتوسط الحسابي بما أن

فالتوزيع ذو التواء موجب مائل نحو اليمين.

4.

1.4 عدد العائلات التي تضم على الأقل 4 أطفال من الجدول السابق هو:

2.4 عدد العائلات التي تضم أقل من 4 أطفال من الجدول السابق هو:

1.5عدد العائلات التي تحتوي على الأكثر على 3 أطفال هو:

2.5 عدد العائلات التي تضم أكثر من 3 أطفال هو:

حل التمرين الثاني:

نستخدم علاقة Pearson المعرفة كما يلي:

1- حساب المتوسط الحسابي:

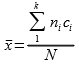
حيث Ci تعبر عن مراكز الفئات

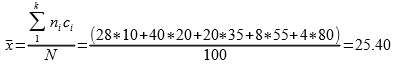
2- حساب المنوال:

بما أن أطوال الفئات غير متساوية ينبغي حساب التكرارات المعدلة، كما في الجدول السابق، باستخدام العلاقة التالية:

بعدها نقوم بتحديد الفئة المنوالية: وهي الفئة التي يقابلها أكبر تكرار معدل =4

ومنه الفئة ]25-15] فئة منوالية.

بعدها نقوم بحساب المنوال بالعلاقة:

3- حساب الوسيط باستخدام علاقة Pearson

4- عدد الأشخاص الذين تقل أعمارهم عن 45 سنة هو

5- عدد الأشخاص الذين تساوي أو تزيد أعمارهم عن 25 سنة هو