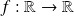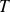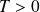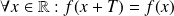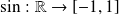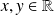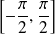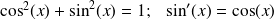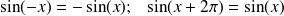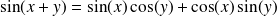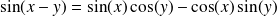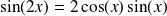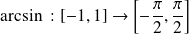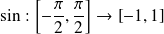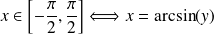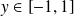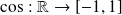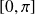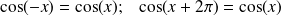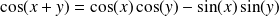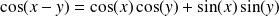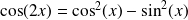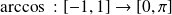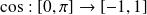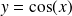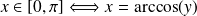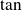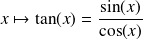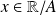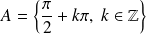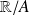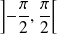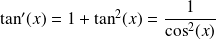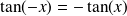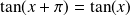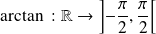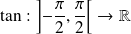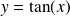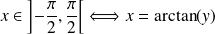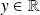Notions de fonction
Définition générale
Définition :
On dit que
 est une fonction[1] réelle si
est une fonction[1] réelle si
 est une application[2] définie sur un sous-ensemble
est une application[2] définie sur un sous-ensemble
 de
de
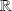 et à valeur dans un sous-ensemble
et à valeur dans un sous-ensemble
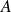 de
de
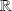 qui associe à tout élément
qui associe à tout élément
 de
de
 un unique élément de
un unique élément de
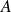 , appelé alors image de
, appelé alors image de
 et noté
et noté
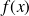 , on écrit
, on écrit
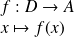
L'ensemble
 est appelé ensemble de départ et
est appelé ensemble de départ et
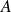 est l'ensemble d'arrivée .
est l'ensemble d'arrivée .
Les éléments de
 qui ont une image par
qui ont une image par
 forment l'ensemble de définition de
forment l'ensemble de définition de
 , noté
, noté
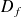 .
.
Exemple :
La fonction
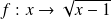 est définie pour tout
est définie pour tout
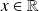 tel que
tel que
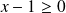 . Donc
. Donc
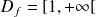 .
.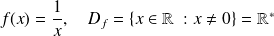 .
.
Graphe d'une fonction
Définition :
On appelle graphe, ou courbe représentative, d'une fonction f définie sur un intervalle
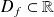 , l'ensemble des points
, l'ensemble des points
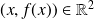 du plan muni d'un repère orthonormé
du plan muni d'un repère orthonormé
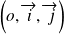 défini par
défini par
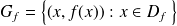 .
.
Fonctions bornées et monotones
Définition :
Soit
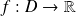 une fonction. On dit que :
une fonction. On dit que :
 est majorée sur
est majorée sur
 si
si
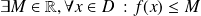 .
. est minorée sur
est minorée sur
 si
si
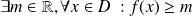 .
. est bornée sur
est bornée sur
 si f est à la fois majorée et minorée sur
si f est à la fois majorée et minorée sur
 , c'est-à-dire si
, c'est-à-dire si
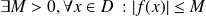 .
.
Définition :
Soit
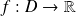 une fonction. On dit que :
une fonction. On dit que :
 est croissante sur
est croissante sur
 si
si
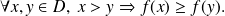
 est décroissante sur
est décroissante sur
 si
si
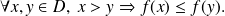
 est monotone (resp. strictement monotone) sur
est monotone (resp. strictement monotone) sur
 si
si
 est croissante ou décroissante (resp. strictement croissante[3] ou strictement décroissante[4]) sur
est croissante ou décroissante (resp. strictement croissante[3] ou strictement décroissante[4]) sur
 .
.
Exemple :
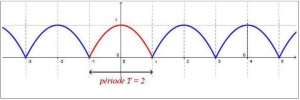
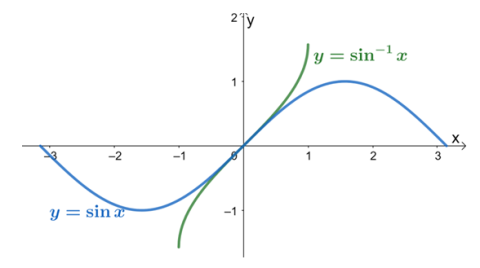
La fonction cosinus
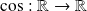 est bornée
est bornée
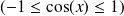 .
.La fonction
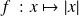 définie sur
définie sur
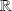 n'est pas monotone.
n'est pas monotone.
Parité et périodicité
Définition :
Soit
 un intervalle de
un intervalle de
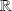 symétrique par rapport à 0[5]. Soit
symétrique par rapport à 0[5]. Soit
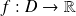 une fonction. On dit que :
une fonction. On dit que :
 est paire si
est paire si
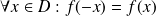 . Son graphe est alors symétrique par rapport à l'axe des ordonnées
. Son graphe est alors symétrique par rapport à l'axe des ordonnées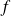 est impaire si
est impaire si
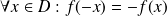 . Son graphe est alors symétrique par rapport à l'origine
. Son graphe est alors symétrique par rapport à l'origine
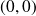 .
.
Exemple :
La fonction définie sur
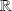 par
par
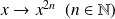 est paire.
est paire.La fonction définie sur
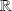 par
par
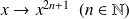 est impaire.
est impaire.
Exemple :
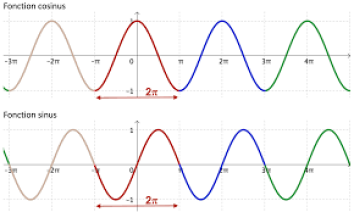
Les fonctions sin et cos sont
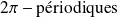 . La fonction tangente est
. La fonction tangente est
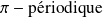 .
.
Composition de deux fonctions
Définition :
Soient
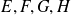 des sous-ensembles de
des sous-ensembles de
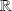 et
et
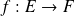 et
et
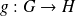 deux fonctions.
deux fonctions.
Si l'espace d'arrivée
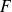 de
de
 est inclus dans l'espace de départ
est inclus dans l'espace de départ
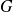 de
de
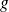 alors on définit la fonction composée
alors on définit la fonction composée
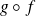 par
par
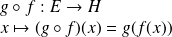 .
.
Exemple :
On considère les fonctions :
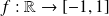 tel que
tel que
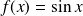 et
et
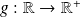 tel que
tel que
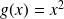
Alors
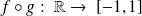 tel que
tel que
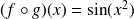
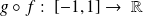 tel que
tel que
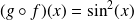
Bijectivité et fonction réciproque
Une fonction
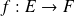 est dite bijective si pour tout point
est dite bijective si pour tout point
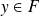 possède un unique antécédent
possède un unique antécédent
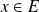 par la fonction
par la fonction
 .
.
Autrement dit
 est bijective si et seulement si
est bijective si et seulement si
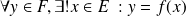 .
.
Exemple :
La fonction
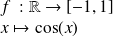 n'est pas bijective car
n'est pas bijective car
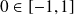 admet au moins deux antécédents dans son espace de départ:
admet au moins deux antécédents dans son espace de départ:
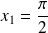 et
et
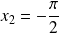 .
.
La fonction
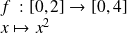 est bijective car pour tout
est bijective car pour tout
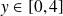 , il existe un unique
, il existe un unique
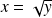 dans l'espace de départ
dans l'espace de départ
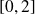 .
.
Définition :
Si une fonction
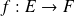 est bijective alors il existe une fonction
est bijective alors il existe une fonction
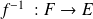 appelée fonction réciproque de
appelée fonction réciproque de
 donnée par
donnée par
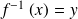 si et seulement si
si et seulement si
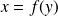 .
.
Proposition
Soient
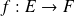 une fonction bijective et
une fonction bijective et
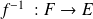 sa réciproque. Alors
sa réciproque. Alors
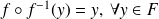 et
et
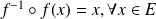 .
.
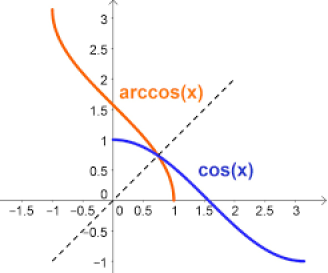
Exemple :
Soit
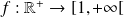 tel que
tel que
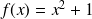 est bijective. Sa fonction réciproque est
est bijective. Sa fonction réciproque est
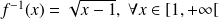 .
.