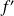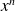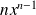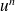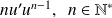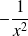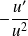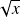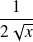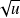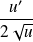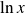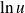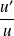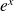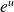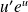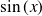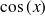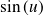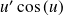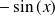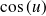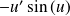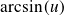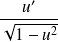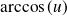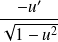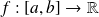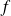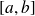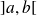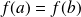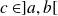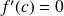Fonction dérivable
Définition :
Soient une fonction
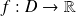et
un point de
.
On dit que
est dérivable au point
si la limite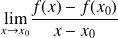
existe et est fini. Cette limite s'appelle la dérivée de
en
et se note
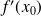.On dit que
est dérivable sur
si
est dérivable en tout point de
.
Remarque :
Si on pose
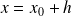, alors la limite précédente donnée par
.
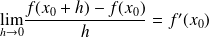Exemple :
Soit
une fonction définie sur
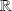par
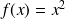. Alors La dérivée de
en un point
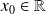est
.
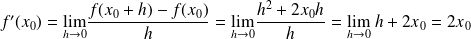Définition : Dérivée à droite, dérivée à gauche
On dit que la fonction
est dérivable à droite en
si
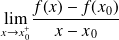existe et est finie. On note, dans ce cas :
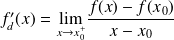.On dit que la fonction
est dérivable à gauche en
si
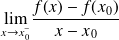existe et est finie. On note, dans ce cas :
.
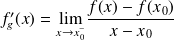Remarque :
La dérivée de
au point
existe si et seulement si
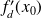et
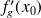existent et sont égales.
.
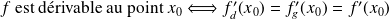Exemple :
Soit
une fonction définie sur
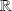par
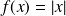, sa dérivée en
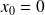n'existe pas car
.
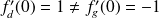Définition : Tangente en un point
Soit
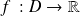une fonction dérivable en un point
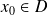. Une équation de la tangente à la courbe de
au point
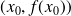est donnée par
.
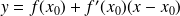Opérations de dérivations
Soient
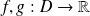dérivables sur
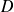. Alors pour tout
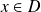, on a
.
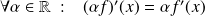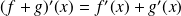
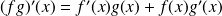.Si
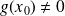, on a
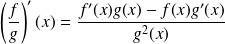. En particulier
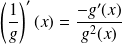.Dérivée de la composée de deux fonctions
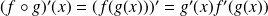.Dérivée de la puissance d'une fonction
.
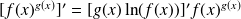Dérivée de fonctions usuelles
Fonction
| Dérivée
| Fonction
| Dérivée
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
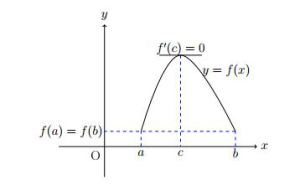
Fondamental : Théorème de Rolle
Soit
Alors il existe au moins un point
|  |
Fondamental : Règle de l'Hôpital
Soient
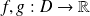deux fonctions continues et dérivables sur
telles que pour tout
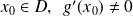. Si
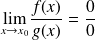ou bien
.
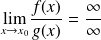Alors,
.
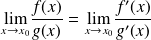Si cette limite tend de nouveau vers
ou
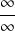, on répète la règle.
Cette règle est applicable aussi pour les limites à l'infini.
Exemple :
Soit la fonction
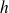définie par
.
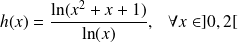Posons
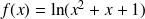et
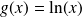alors
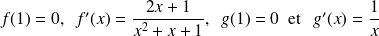. On a
,
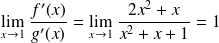d'après la règle de l'hôpital,
.
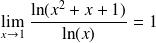