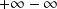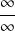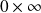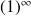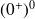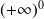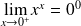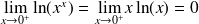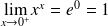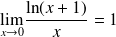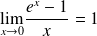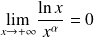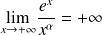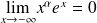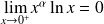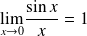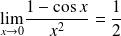Limite d'une fonction
Soit
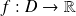une fonction définie sur un intervalle
de
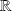. Soit
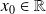un point de
ou une extrémité de
.
Définition : Définition générale de la limite
Soit
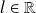. On dit que
a
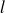pour limite en
si,
.
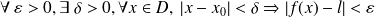On écrit dans ce cas,
.
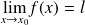Complément : Unicité de la limite
Si la limite de
au point
existe alors cette limite est unique.
Limite à droite, limite à gauche
Soit
une fonction définie sur un intervalle
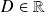
la fonction
admet
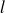comme limite à droite de
notée par
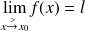, ou bien
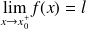.la fonction
admet
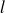comme limite à gauche de
notée par
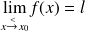, ou bien
.
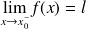Remarque :
Si la fonction
admet une limite
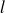à gauche du point
et une limite
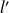à droite de
, pour que
admet une limite au point
il faut et il suffit que
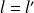. C'est-à-dire
.
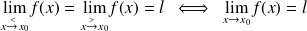Exemple :
Considérons la fonction définie sur
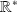par
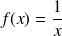
On a
.
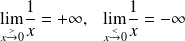Alors,
n'admet aucune limite au point
.
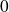Opérations sur les limites
Soient
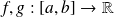et
.
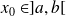Supposons que
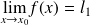et
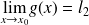, alors
.
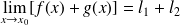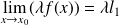, pour tout
.
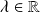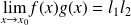.Si
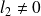et
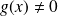alors
.
.
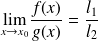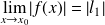Remarque : Voici une liste des formes indéterminées (FI):
|
|
|
|
|
|
|
Rappel : Quelques limites à connaître
Pour tout
|
|
|
|
|
|
|
|
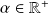
