Continuité d'une fonction
Définition :
Soient une fonction
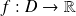 et
et
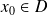
 est dite continue au point
est dite continue au point
 si
si
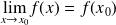 .
. est continue sur
est continue sur
 si elle est continue en tout point de
si elle est continue en tout point de
 .
.
Exemple :
Les fonction sinus et cosinus sont continues sur tout
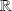 .
.Les fonctions polynômes sont continues sur tout
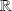 .
.
La continuité à droite et à gauche
Soit
 une fonction définie sur un intervalle
une fonction définie sur un intervalle
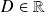
La fonction
 est dite continue à droite en
est dite continue à droite en
 si
si
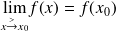 .
.La fonction
 est dite continue à gauche en
est dite continue à gauche en
 si
si
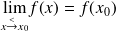 .
.
Remarque :
La fonction
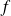 est continue en
est continue en
 si et seulement si
si et seulement si
 est continue à gauche et à droite du point
est continue à gauche et à droite du point

 .
.
Exemple :
Soit la fonction
 définie par
définie par
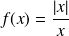 si
si
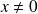 et
et
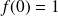 est continue sur
est continue sur
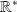 . Au point
. Au point
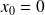 , la fonction
, la fonction
 est continue à droite , mais elle ne l'est pas à gauche car
est continue à droite , mais elle ne l'est pas à gauche car
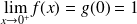 et
et
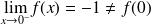 .
.
Opérations sur les fonctions continues
Soient
 et
et
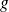 deux fonctions définies sur
deux fonctions définies sur
 . Si
. Si
 et
et
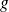 continues en un point
continues en un point
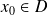 , alors
, alors
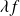 est continue en
est continue en
 , pour tout
, pour tout
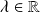
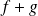 est continue en
est continue en
 .
.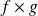 est continue en
est continue en
 .
.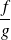 (si
(si
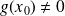 ) est continue en
) est continue en
 .
.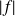 est continue en
est continue en
 .
.
Fondamental : Théorème des valeurs intermédiaires
Soient
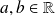 et
et
 une fonction de
une fonction de
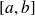 dans
dans
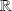 .
.
Si
 est continue sur
est continue sur
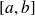 .
.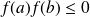 .
.
Alors il existe
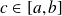 tel que
tel que
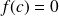 . (Autrement dit l'équation
. (Autrement dit l'équation
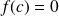 admet au moins une solution dans
admet au moins une solution dans
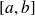 ).
).
Exemple :
La fonction
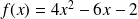 admet une solution dans l'intervalle
admet une solution dans l'intervalle
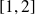 . En effet,
. En effet,
 est continue sur
est continue sur
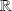 car elle est polynôme.
car elle est polynôme.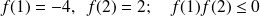 .
.
Donc il existe
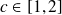 tel que
tel que
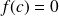 .
.






