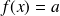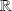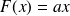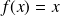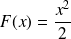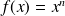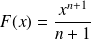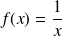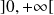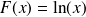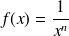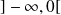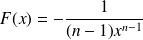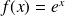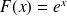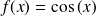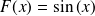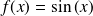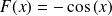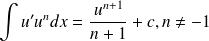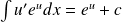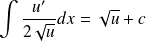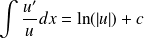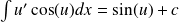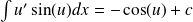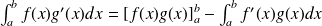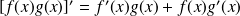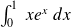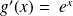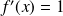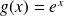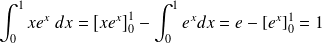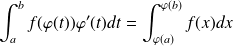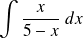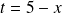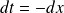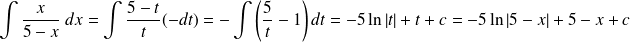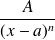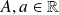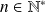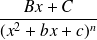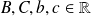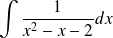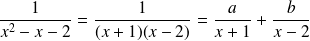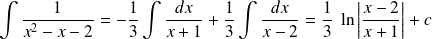Intégration
Définitions
Définition :
Soit
une fonction définie sur un intervalle
, on appelle primitive de
sur
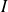, toute fonction
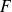définie et dérivable sur
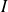, vérifiant :
.
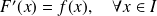Exemple :
Soit la fonction
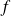définie sur
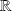donnée par :
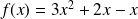. Sa fonction primitive est
.
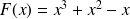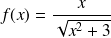. Sa fonction primitive est
.
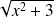Propriétés de la primitive
Soit
une fonction définie et admet une primitive sur
alors
-
admet une infinité de primitives sur
.
Si
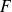est une primitive de
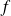il en est de même de
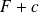ou
est une constante.Si
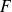et
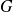sont deux primitives de
sur un intervalle
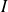, alors il existe un réel
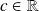tel que
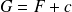.Soit
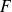est une primitive de
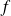et soit
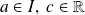, donc il existe une unique primitive
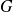de
qui vérifie
.
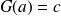Définition :
L'ensemble de toutes les primitives de la fonction
est appelé intégrale indéfinie, notée par
.
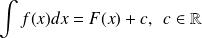Exemple :
.
.
.
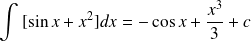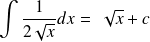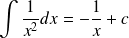Fondamental : Théorème d'existence de l'intégrale
Si la fonction
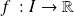définie et continue sur
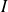, alors
admet une primitive sur
.
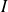Quelques primitives usuelles
Fonction | Ensemble de definition | Primitive |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Soit
est une fonction, alors
|
|
|
|
|
|
Définition :
on appelle l'intégrale définie de
sur
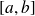le nombre réel
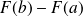où
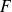est une primitive de
on le note
.
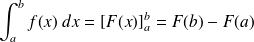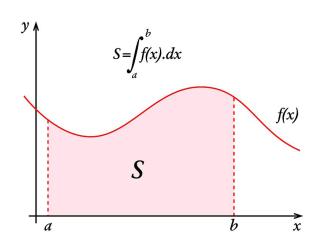
Exemple :
.
.
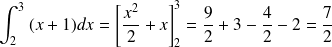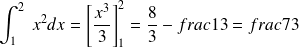Propriétés de l'intégrale
Soient
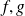des fonctions intégrables sur
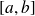et
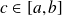. Alors on a :
.
.
.
.
.
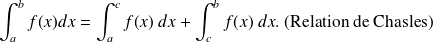
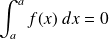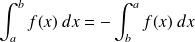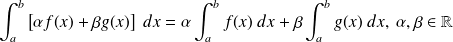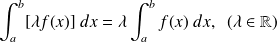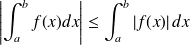Méthodes de calcul intégrales
1. Calcul à l'aide des primitives
Exemple :
Calculer l'intégrale suivants :
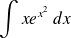
On remarque que
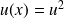, comme
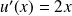, on écrit
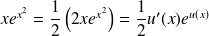. Alors
.
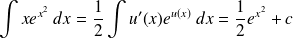