Aperçu des sections

  • Généralités

    Tout replier Tout déplier

  • Fundamentals of Operations Research - LECTURES and DIRECTED WORKS -

    SECOND YEAR FILA STUDENTS

    FINANCE DEPARTMENT



  • Live stream teaching ( Videoconferencing)


  • Contact Information 

    Module: Fundamentals of Operations Research

    Academic Year: 2024/2025

    Level: L2 (International Finance-Applied English Language Studies, Double License Students)

    University: Abou-Bekr Belkaid Tlemcen

    Faculty of Economic and Management sciences

    Department of Accounting and Finance

    Lecturer: Dr. MELLOUL Sakina

    Tutor: Dr. MELLOUL Sakina

    Email address: sakina.melloul@univ-tlemcen.dz

    Teaching Unit: Methodology

    Coefficient: 02

    Credits: 04

    Semester : Fourth semester

    Semester hours : 15 weeks/ 45 HOURS

    Weekly volume: 3 hours/ week - Lectures and Directed works-

    Evaluation method: General average= (examination ×0.6)+( continious assessment ×0.4)

    • Exam : The grade from the end of semester exam
    • Continuous monitoring= (Presence+ Test+ homework)/3
    • Attendance= 20 - ( number of unjustified absences ×5)- (number of justified absences × 2)

    Follow-up modality (Tutoring schedule):
    Monday: 10h00-11h30
    Tuesday: 10h00- 11h30

      

  • NEWS FORUM


  • Educational objectives of the course

    By the end of the semester, the student will be able to:

    1-Remembering

    •  Define key terms such as operations research, linear programming, and simplex method.
    •  Recall the steps involved in formulating a linear programming model.

    2- Understanding

    •  Explain the significance of operations research in decision-making.
    •  Describe the components of a linear programming problem, including objective functions and constraints.

    3- Applying

    •  Apply linear programming techniques to solve real-world problems.
    •  Use graphical methods to determine feasible solutions for two-variable problems.

    4- Analyzing

    •  Analyze a given problem to identify constraints and decision variables.
    •  Compare different optimization techniques (e.g., simplex vs. graphical method).

    5- Evaluating

    • Evaluate the effectiveness of various operations research methods in different scenarios.
    •  Assess the outcomes of linear programming models and make recommendations based on sensitivity analysis.

    6- Creating

    •  Design a comprehensive linear programming model for a complex organizational problem.
    •  Formulate new approaches to optimize resource allocation using operations research techniques.

  • Prerequisite and test prereqisites

    To study the Operations Research course, the student should have the prerequisite knowledge over:

    1. Basic Mathematics:

    • Linear algebra: vectors, matrices, linear systems.

    • Basic limits and derivatives.

    • Equations and inequalities.

    2. Descriptive Statistics and Probability:

    • Means, standard deviation, dispersion.

    • Basic probability and simple distributions.

    3. Mathematical Modeling Skills:

    • Ability to transform a real-world problem into mathematical equations.

    • Understanding relationships between variables and constraints.

    4. Basic Programming or Computer Skills:

    • Using Excel (especially Solver).

    • Ability to follow algorithmic steps logically.

    5. Analytical Thinking Skills:

    • Systematic problem-solving.

    • Analyzing alternatives and making decisions.


  • GENERAL COURSE PLAN

    • General objectives

    • Contact form

    • Pre-requisites and test of the pre-requisites

    • General Introduction

    • Chapter 01: Introduction to Operations Research

    • Chapter 02: Mathematical formulation of the linear programming model.

    • Chapter 03: The Graphical Method for solving LPM.

    • Chapter 04: The SIMPLEX method for solving LPM.

    • Chapter 05: Duality theory.

    • Chapter 06: Transportation Problems.

    • Post-tests and remediation method

    • References



  • MENTAL MAP

    Marqué

  • GENERAL INTRODUCTION TO THE COURSE


    Introduction:

     The Fundamentals of Operations Research Module designed for second-year undergraduate students (International Finance & Applied English) represents a valuable opportunity for them to learn mathematical techniques that researchers use to make important decisions in organizations. This involves identifying the best use of available resources, whether they are financial or human. Moreover, operations research techniques are applied in various fields such as industry, commerce, and services.

    The overall goal of this educational material is to equip students with some guiding techniques used by operations research (linear programming) to solve problems within organizations. The skills aimed to be achieved through this educational material include the ability to achieve organizational goals using various linear programming models.

    🗝️ Key Words:

    Linear programming, Mathematical formulation, Simplex method, Graphical method, Transportation problems. Duality.

  • Chapter 01: Introduction to Operations Research

    🔍Short Description:


    This chapter presents an introductory chapter to Operations Research. It defines the field, outlines its historical development from military origins to modern applications, and introduces its core concepts such as mathematical modeling, optimization methods, deterministic and stochastic models, simulation, queuing theory, network analysis, and inventory control.

    🎯 Specific Objectives:

    By the end of this chapter, students bshoukd be able to:

    1. Present a clear definition of Operations Research and its scientific foundation.

    2. Explain the historical origins and evolution of OR from World War II to civilian industries.

    3. Introduce fundamental OR concepts, including models, optimization techniques, and analytical tools.

    4. Describe key application areas where OR improves decision-making and system performance, such as supply chains, scheduling, finance, and healthcare.


  • Chapter 02:Mathematical formulation of the linear programming model

    🔍Short Description:


    This chapter introduces the mathematical formulation of Linear Programming (LP). It explains the definition of LP, its key components (decision variables, objective function, constraints, non-negativity), and provides a systematic procedure to translate a real-world problem into a linear programming model. The chapter also includes an applied example to illustrate the complete formulation process.

    🎯 Specific Learning Objectives:


    After studying this chapter, the student will be able to:

    1. Define linear programming and explain its purpose in optimization.

    2. Identify decision variables relevant to a real-world optimization problem.

    3. Formulate an objective function for maximization or minimization.

    4. Translate resource, demand, and technical conditions into linear constraints.

    5. Apply the non-negativity requirements to all decision variables.

    6. Construct a complete linear programming model from a descriptive problem statement.

    7. Analyze a practical case and derive the correct LP formulation step by step.


  • Chapter 03: The Graphical Method for solving LPM

    🔍Short Description:


    This chapter explains the graphical method used to solve linear programming problems with two decision variables. It presents the step-by-step procedure for plotting constraints, identifying the feasible region, determining corner points, and evaluating the objective function graphically. An illustrative example demonstrates how to obtain the optimal solution visually.

    🎯 Specific Learning Objectives:


    After completing this chapter, the student will be able to:

    1. Describe the purpose and limitations of the graphical method in linear programming.

    2. Formulate a linear programming problem suitable for graphical analysis.

    3. Construct a coordinate system and plot constraint lines accurately.

    4. Identify the feasible region that satisfies all constraints.

    5. Determine corner (vertex) points of the feasible region.

    6. Compute the objective function value at each corner point.

    7. Select the optimal solution (maximum or minimum) based on graphical evaluation.


  • Chapter 04: The SIMPLEX method for solving LPM

    🔍Short Description:

    This course provides a concise introduction to the Simplex Method for solving linear programming problems. It covers the formulation of optimization models, graphical interpretation, and step-by-step application of the simplex algorithm to maximize or minimize objective functions under constraints. The course emphasizes practical problem-solving skills and interpretation of results in economic and operational contexts.

    🎯 Specific Objectives:

    By the end of this course, learners will be able to:

    1. Formulate real-world optimization problems as linear programming models.

    2. Identify decision variables, objective functions, and constraints accurately.

    3. Convert linear programming problems into standard and canonical forms.

    4. Apply the Simplex Method step by step to solve maximization and minimization problems.

    5. Interpret simplex tableaux and understand pivot operations.

    6. Analyze optimal solutions, including feasibility and optimality conditions.

    7. Interpret the economic meaning of results (e.g., resource allocation and shadow prices).

    8. Solve practical problems related to economics, management, and operations research.

  • Chapter 05: Duality Theory

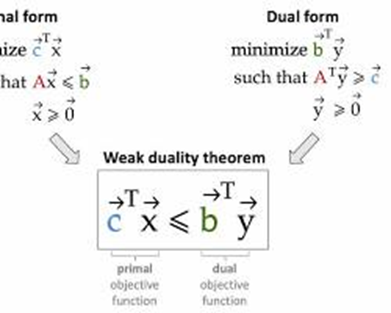
    🔍Short Description:

    This course introduces the concept of duality in linear programming, explaining the relationship between primal and dual problems. It focuses on formulating dual models, understanding their economic interpretation, and analyzing optimal solutions using duality theory. The course highlights the role of duality in sensitivity analysis and decision-making.

    🎯 Specific Objectives:

    By the end of this course, learners will be able to:

    1. Formulate the dual of a given linear programming problem.

    2. Understand the relationship between primal and dual problems.

    3. Interpret the economic and operational meaning of dual variables.

    4. Apply duality to analyze and verify optimal solutions.

    5. Use duality for sensitivity analysis and decision-making.

    6. Solve practical problems in resource allocation, cost minimization, and profit maximization using duality concepts.

  • Chapter 06: Transportation Problems.

    🔍Short Description:

    This course covers transportation problems in linear programming, focusing on optimizing the distribution of goods from multiple sources to multiple destinations at minimum cost. It emphasizes problem formulation, solution methods, and practical applications.

    🎯 Specific Objectives:

    By the end of this course, learners will be able to:

    1. Formulate transportation problems as linear programming models.

    2. Identify supply, demand, and cost parameters accurately.

    3. Apply methods such as the Northwest Corner Rule, Least Cost Method, and Vogel’s Approximation to find initial feasible solutions.

    4. Use the stepping-stone or MODI method to optimize transportation costs.

    5. Analyze and interpret optimal transportation plans.

    6. Solve real-world logistics and distribution problems efficiently.

  • Post- Tests and remediation method


  • GENERAL CONCLUSION

    Conclusion : résultats (56 mille) d’images libres de droits, de photos de stock et d’illustrations | Shutterstock

    The course Fundamentals of Operations Research provides learners with essential analytical tools for rational decision-making in complex systems. Through the study of linear programming, the simplex method, duality, and transportation problems, the course develops the ability to model real-world situations, analyze constraints, and identify optimal solutions. Overall, this course builds a strong methodological foundation that supports efficient resource allocation, problem-solving, and strategic planning in economics, management, and operational contexts.


  • 📚 Key Bibliographic References

    References:

    1. A. M. Natarajan, P. Balasubramanie, A. Tamilarasi, (2016), « Operations Research», Second Edition, Pearson.

    2. Colin Palmer and Alexander E. Innes, (1980), «Operations Research by example». The MACMILLAN Press LTD. London and Basingstoke.

    3. Er. Prem Kumar Gupta, D. S. Hira, (2014)., «Operations Research». S. CHAND. New Delhi.

    4. H. A. Eiselt. C & L. Sandblom, (2007). « 7Linear Programming and its Applications». Springer.

    5. Nita H. Shah, Ravi M. Gor, Hardik Soni. (2010). «Operations Research». Eastern Economy Edition. New Delhi.

    6. P. Rama Murthy. (2007). « Operations Research». Second Edition. New Age International Publishers. New Delhi.

    7. Robert J. Vanderbei, (2020). « Linear Programming, Fondations and Extensions». International Series in Operations Research & Management Science. Fifth Edition. Springer.

    8. Frederick S. Hillier, Gerald J. Lieberman(2014), «Introduction to Operations Research»,  Mc Graw-Hill.